“Физический парадокс это некий вывод из теории, который противоречит другим выводам из неё же, или реальным наблюдениям”. Вообще-то выявление любого парадокса должно бы заставить нормального человека просто отвергнуть любую теорию, но люди заявляющие себя физиками не настолько нормальны чтобы так поступить, и физика стала кучей теорий практически не связанных с реальностью…
Парадокс Гиббса был создан для иллюстрации теорий квантовой механики, когда реальные наблюдения Гиббса были математизированы и эти математические упражнения стали обыгрывать мысленными экспериментами. Суть парадокса проста. Если дать смешаться двум газам с разной энергией, то общая их энергия уменьшится. (Растет энтропия.) Это как бы отразили формулой: S=N CV
ln(T )+k N ln(
V
N )
(1),
где
S – энтропия,
N — количество частиц,
CV – теплоёмкость при постоянном объёме,
T – температура,
k — постоянная Больцмана,
V – объём.
По формуле получилось, что не имеет значения какие газы смешиваются, результат одинаков. Парадокс получился когда смешали два одинаковых объёма то одинаковых, то разных газов с одинаковыми T и N. Например, между ними сначала есть перегородка, потом её убирают. В первом случае смешивают два одинаковых газа; во втором – два почти не отличающихся но различных газа. Получаются энтропии с разницей в 2k N ln(2) (2) .
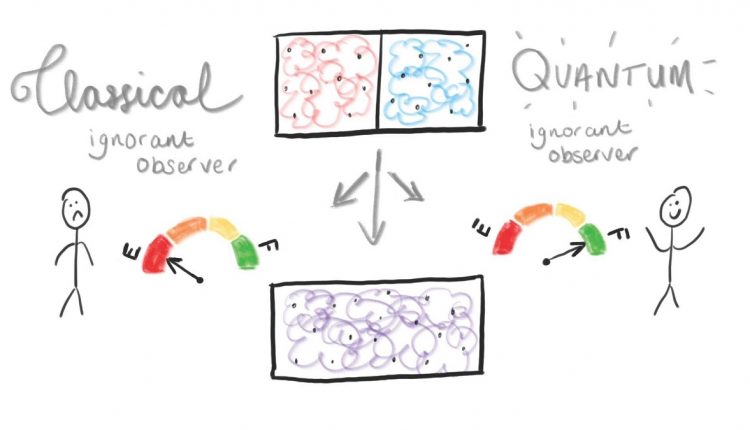
Ещё раз надо подчеркнуть, что все эти упражнения мысленные, то есть математические. Вариантов этой галиматьи невероятно много. Вот очередной такой вариант: Математики из Ноттингемского университета применили новую квантовую теорию к парадоксу Гиббса и продемонстрировали фундаментальное различие в роли информации и управления между классической и квантовой термодинамикой. Их фантазии были опубликованы в журнале Nature Communications. Они мысленно проверили теорию, основанную на смешивании двух квантовых (то есть фантастических) газов – например, красного и синего, в остальном идентичных, которые сначала разделяются, а затем смешиваются в коробке. В целом система стала более однородной, что количественно выражается увеличением энтропии. Если затем наблюдатель наденет фиолетовые очки и повторит процесс; газы выглядят одинаково, поэтому кажется, что ничего не меняется. В этом случае изменение энтропии равно нулю.
Ведущие авторы статьи, Бенджамин Ядин и Бенджамин Моррис, объясняют: “Наши выводы кажутся странными, потому что мы ожидаем, что физические величины, такие как энтропия, имеют значение независимо от того, кто их вычисляет.
Ну и дальше обычный бред интерпретации характерный для теоретиков: “Рассматривая ситуацию, когда система становится большой, где квантовое поведение обычно исчезает, исследователи обнаружили, что квантовый невежественный наблюдатель может извлечь столько же работы, как если бы он был в состоянии различить газы. Управление этими газами с помощью большого квантового устройства вело бы себя совершенно иначе, чем классический макроскопический тепловой двигатель. Это явление является результатом существования специальных суперпозиционных состояний, которые кодируют больше информации, чем доступно классически”. “Квантовые тепловые двигатели – это микроскопические версии наших повседневных нагревателей и холодильников, которые могут быть реализованы только с одним или несколькими атомами (что уже экспериментально подтверждено) и производительность которых может быть повышена с помощью подлинных квантовых эффектов, таких как суперпозиция и запутывание”.
Весь бред в формуле, а не в реальном мире. Длина свободного пробега частиц равна:
L=
1
√2σ
N
V
(3),
где
L — длина свободного пробега частиц,
σ — площадь поперечного сечения одной частицы.
Тогда формула (1) преобразуется к виду:
S=N CV
ln(T )+k N ln(√2σ L) (4).
Площадь эффективного сечения (σ) равна у похожих частиц.
А длина свободного пробега (L) задаётся как столкновениями
одинаковых, так и разных частиц, поэтому при одинаковых количествах всех частиц и одинаковых занимаемых объёмах не изменяется.
Следовательно и энтропии этих газов ведут себя одинаково.
