В предисловии к статье “О специальной и общей теории относительности” написанной в 1916 году, Эйнштейн отмечает, что работа “…имеет целью дать наиболее точное представление о теории относительности читателям, интересующимся этой теорией с общенаучной, философской точки зрения…Автор приложил много усилий для того, чтобы достигнуть по возможности более ясного и простого изложения основных мыслей в той последовательности и связи, в какой они фактически возникли” [36, с.167].
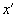
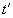
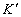
Проанализируем “простой вывод преобразований Лоренца” [36, с.223-226], выполненный лично автором релятивизма, который отражает ход его мыслей “в той последовательности, в которой они фактически возникли“. В нем дается решение задачи определения параметров движения и в подвижной системе , если известны соответствующие параметры x и tнеподвижной системы K (рис.25).
Весь вывод построен на основе дикого произвола в логике с нарушением элементарных правил алгебры, при которых в школах ученики получают двойки.
Эйнштейн знал преобразования Лоренца, и, не отличаясь серьезными знаниями физики и математики, шел с конца, опираясь на метод проб и ошибок, который в его руках превращался в метод свободной игры в понятия, равносильный искажению реальной картины явлений.
Он взял готовые преобразования Лоренца, и стал думать, как создать “теорию”.
Ему не составило большого труда представить первое и четвертое преобразование Лоренца в следующем виде:
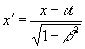
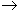
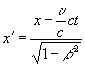
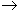
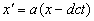
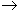
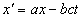
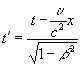
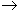
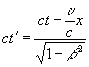
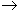
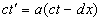
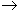
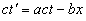
.
Отсюда имеем
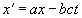
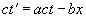
, , (18.1)
где заранее известно, что
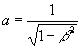
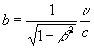
и . (18.1а)
Кроме того, первое преобразование Лоренца он представлял в следующих возможных вариантах:
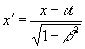
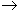
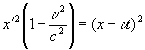
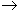
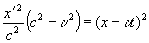
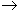
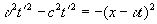
или
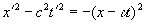
. (18.1b)
Конечно, трудно сказать, как долго он колдовал над данными преобразованиями. Мы это никогда не узнаем, но то, что он шел этим путем, сомнений нет.
Теперь оставалось “сообразить теорию”.
Рассмотрим, как она соображалась, считая, для определенности, неподвижную систему отсчета K физической системой (пусть это будет железная дорога с окружающим воздушным пространством на Земле), а подвижную систему отсчета будут попеременно представлять физическая и пустая системы отсчета (пассажирский вагон и железнодорожная платформа). Такая двойственность необходима для более полного анализа алогичных схоластий “теоретика”.
Первая схоластия.
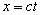
“Световой сигнал, распространяющийся в положительном направлении оси Х, движется в соответствии с уравнением , или
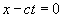
. (1)
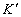
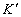
Так как этот же световой сигнал распространяется и относительно (предполагается, что световой сигнал возникает в тот момент, когда начала координат обоих систем совпадали. – Л.К.) с той же световой скоростью с (в подвижной системе координат скорость сигнала неподвижной системы относительна независимо от типа подвижной системы. – Л.К.), то его движение относительно системы будет описываться уравнением
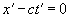
. (2)
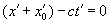
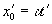
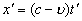
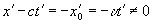
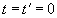
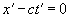
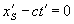
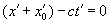
(Если описывать относительное движение фронта волны неподвижной системы через параметры подвижной системы на основании абсолютной скорости неподвижной системы, то , где – положение начала координат подвижной системы (рис.24а), или же . Поэтому , и лишь когда имеет место равенство: ; если же система физическая, то и в ней возникает сферическая волна, и тогда (рис.24b). Таким образом, уравнение (2) не верно, а верно уравнение . – Л. К.)
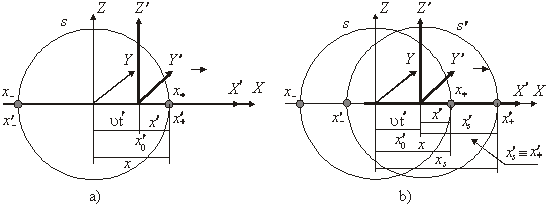
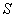
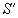
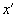
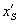
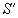
Рис.24. а) Физическая система с фронтом волны S и пустая система без собственного фронта волны; b) физические системы; – фронт волны пространства неподвижной системы, – фронт волны пространства подвижной системы, x и – координаты фронта волны S соответственно в неподвижной и подвижной системах, – координата фронта волны в подвижной физической системе.
Пространственно-временные точки (события), удовлетворяющие уравнению (1), должны удовлетворять также уравнению (2). Это, очевидно, будет иметь место в том случае, если вообще выполняется соотношение
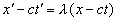
, (3)
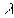
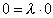
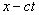
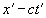
где – некоторая постоянная (это оригинальная игра в нолики, так как . – Л.К.). В самом деле, согласно соотношению (3), обращение в нуль выражения означает обращение в нуль и (а разве они не нули? – Л.К.).
Совершенно аналогичное рассуждение, примененное к световым лучам, распространяющимся в отрицательном направлении оси Х, приводит к условию
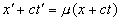
(4)”
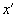
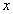
Здесь Эйнштейн совершает подмену символов, ибо координаты и , входящие в уравнение (4), и координаты с такими же символами уравнения (3) относятся к противоположным точкам сферической волны, поэтому уравнения (3) и (4) необходимо записать так:
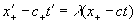
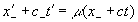
, . (18.2)
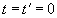
Индексы “+ ” и “- ” отмечают противоположные координаты точек на оси X (рис.24b). Кроме того, как выше уже отмечалось, они верны лишь для случая .
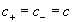
По Эйнштейну в подвижной системе , и в этом смысле она физическая система, поэтому неверные уравнения (3) и (4) следовало представить в виде
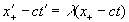
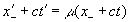
, . (18.2а)
Однако великий комбинатор молча отождествляет противоположные координаты фронта волны подвижной и неподвижной систем координат:
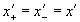
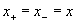
, , (18.3)
хотя у него
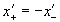
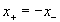
, . (18.3а)
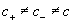
Если подвижная система – пустая, тогда .
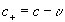
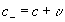
В пустой и физической подвижной системе координат относительная скорость сигнала S в положительном и отрицательном направлении соответственно равна: и , поэтому
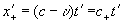
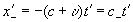
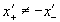
, и . (18.4)
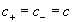
Поскольку Эйнштейн формально полагает , у него
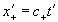
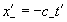
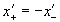
, и . (18.4а)
Обратим еще раз внимание на исходные равенства (3) и (4). Они – детская игра в нолики и крестики:
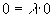
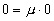
, . (4а)
Нолики – это эйнштейновские уравнения движения
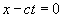
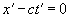
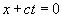
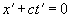
, , , , (4b)
а крестики – умные и с дальним прицелом умножения нулей на формальные множители.
Нет необходимости объяснять, что подобные посылки-равенства – это псевдологические, но весьма тонкие фокусы вопиющего погрома элементарной школьной алгебры, которые обнаружить не просто при массированном воздействии на умы людей.
Вторая схоластия.
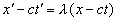
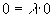
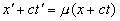
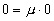
” Складывая и вычитая соотношения (3) и (4) (т.е. складывая и вычитая нули: () и (), где, еще раз напоминаем, координаты обоих уравнений относятся к противоположным точкам фронта волны. – Л.К.) и при этом вводя для удобства вместо постоянных l и m новые постоянные
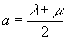
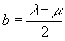
, ,
получаем
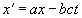
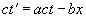
, . (5)
Наша задача была бы решена, если бы были известны постоянные a и b; последние определяются из следующих соображений”.
В книге первое уравнение (5) записано со знаком “+”, что нужно рассматривать как опечатку.
Строго говоря, великий комбинатор должен был складывать уравнения (18.2а), в которых симметричные координаты имеют свои собственные символы, что приводит к уравнению:
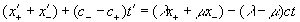
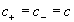
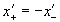
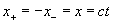
Так как по Эйнштейну , но и , то данное уравнение приобретает вид:
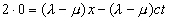
,
или
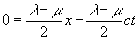
. (18.5)
Если принять
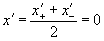
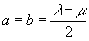
, , (18.6)
получаем эйнштейновское уравнение (5):
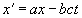
,
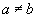
в котором у теоретика релятивизма . Искать логику в данном эйнштейновском равенстве бесполезно – за такие фокусы в хорошей советской школе принято было ставить круглую двойку, а если ребенок так же учился по всем предметам, ему приходилось оканчивать школу для умственно отсталых детей.
Если составить разность уравнений (18.2а), получим
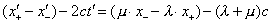
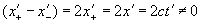
В общем случае, кроме начала координат, , а у Эйнштейна данная разность равна нулю. Примем эту ложь за правду, иначе не придем к уравнению (5а).
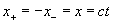
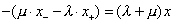
Далее, , поэтому и
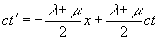
Если принять
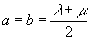
, (18.7)
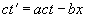
тогда ценой грубейших ошибок, или по существу безграмотных, но преднамеренных действий, получаем второе эйнштейновское уравнение (5): .
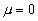
Равенства (18.6) и (18.7) совместимы, если .
Продолжим читать Эйнштейна.
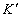
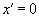
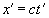
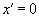
“Для начала координат системы все время (у Эйнштейна что-то плохо с памятью, ибо – есть координата фронта волны, а – есть точка начала координат, и опять совершенно различные координаты обозначены одним символом – это кустарная работа мастера свободной игры в понятия на основе шизологики. – Л.К.), следовательно, согласно первому уравнению (5), имеем
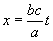
“.
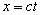
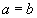
В данном равенстве х есть координата фронта волны, и поэтому , так что получается еще раз: .
Третья схоластия.
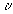
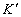
“Обозначая через скорость, с которой начало координат системы движется относительно K, находим
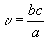
(6)”
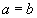
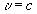
Как мы уже видели, , поэтому из данной формулы следует, что .Четвертая, завершающаяся схоластия с релятивистской алгеброй обратных дробей.
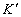
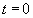
В этой схоластии Эйнштейн предлагает сделать “моментальный снимок” системы из системы K, для чего полагает и “тогда из …уравнения (5) получим
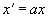
“. (6а)
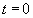
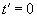
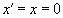
Если , то, как следует из условия задачи, и , т.е. рассматривается начало процесса. На основании (6а) релятивист записывает
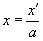
. (7)
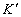
Равенство (7) есть эйнштейновский “снимок-вгляд” из системы K на систему .
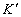
В силу релятивистской равноправности систем эйнштейновский “снимок-вгляд” из системы на систему K требует выражение (7) представить в виде
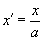
. (7а)
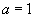
Сравнивая (7) и (7а), видим, что . За данными равенствами скрывается игра в нолики:
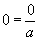
. (18.8)
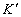
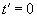
Далее, великий теоретик утверждает, “…если делается моментальный снимок системы K из системы (), то, исключая t из уравнений (5) при помощи равенства (6), получаем
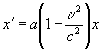
” (18.9)
Явный вид этого уравнения таков:
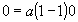
. (18.9а)
Полученное уравнение не поддается комментариям, и подобная “логика” сродни абстракционизму в искусстве, где вам показывают поп-артовский бред эстетов с надломленной психикой.
Соединяя выражения (7а) и (18.9) , Эйнштейн получает
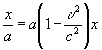
.
Отсюда он приходит формально к долгожданному корню
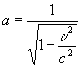
, (18.10)
но за этим равенством скрывается выражение лишенное всякого смысла, ибо
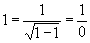
. (18.10а)
Теперь принимая во внимание выражения (18.9), (5) и (6), Эйнштейн записывает
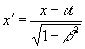
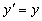
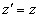
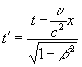
, , , . (18.11)
Так патентовед в XX веке создавал и пропагандировал видимость теории преобразований Лоренца. История науки не знает ничего подобного: человек без серьезных знаний физики и математики, но с умом склонным к логическим извращениям сумел создать видимость научной теории, которая была поддержана в силу ее идеологического характера.
Его деятельность не может сравниться с тысячами современных магов, прорицателей, гадалок, колдунов, и просто аферистов – он всех перещеголял.
Подобная премьера абсурда могла состояться потому, что уже в начале XX века выдающиеся мыслители Европы и России указывали на признаки глубокого кризиса в мире искусства и науки, кризиса духовности, который достаточно грубо, агрессивно себя проявляет на голубых экранах. Кризис рожден позитивизмом-прагматизмом-махизмом-операционализмом, но на это, к сожалению, не обращают должного внимания, и патентовед продемонстрировал всю глубину этого кризиса, отражавшего и глубокий социальный кризис в Европе первых десятилетий XX в., когда в моде было шарлатанство и безумие, и требовались “безумные теории”, т.е. шизотеории, и Эйнштейн одну из таких “теорий” выдал.
Л. Г. Крейдик info@dialectical-physics.org
