Океанов Евгений Николаевич
Теория относительности в двух ее ипостасях – СТО и ОТО – считается надежно проверенной теорией, которая занимает лидирующее место среди прочих теорий. Узнать, в какой мере это оправдано, можно лишь в процессе анализа начальных сведений об этой теории и ее математическом аппарате.
К концу XIX века успехи в развитии математики дали основание ученому сообществу возвести математику в ранг непогрешимости. В это же время физика вплотную подошла к мало понятному микромиру, с которым неизвестно было, что делать. Сегодня кажется очевидным, что переход от макромира к микромиру в первую очередь требует повышения на десятки порядков точности исследований. Это значит, что надо было в теоретических исследованиях отказаться от приближенных (то есть, с точностью до макромира) результатов, для чего такие исследования пересмотреть с повышенной точностью (до микромира). А тогда это было неочевидно. Впрочем, эта задача актуальна и теперь. Так вот, непогрешимая математика и должна была вывести на подходы к мало понятному микромиру, эксперименты с которым в части изучения атомов намекали на планетарную систему элементарных частиц. А это предполагало и связь с космологией. Так обозначился кризис физики к началу ХХ века. Разрешение этого кризиса осуществляется и по сию пору.
До кризиса среда нашего обитания средствами классической математики выражалась в виде понятия трехмерного пространства, которое с параметром в виде времени вполне обеспечило решение множества физических задач теории и практики. А в разрешении кризиса участвует множество различных теорий, наиболее популярной из которых является так называемая теория Большого Взрыва, которая рассматривает нашу среду обитания в четырехмерном пространстве с помощью аппарата тензорного исчисления. Основой этого пространства является так называемый четырехвектор пространства-времени R4:
(1)
Три его измерения и определяют метрику протяженности, а четвертое – t– метрику времени. Это называется задание вектора в аффинных координатах. Классический дифференциал dr4 вектора (1) имеет вид:
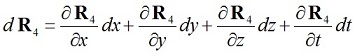(2)
Делением обеих его частей на дифференциал времени dt легко получить выражение скорости V4 в четырехмерном афинном пространстве:
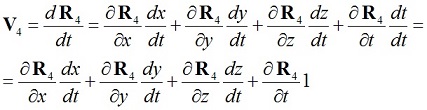(3)
Непосредственное дифференцирование вектора (1) по времени t принимает вид:
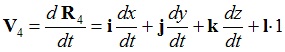(4)
Из сравнения равенств (3) и (4) следуют равенства:
(5)
То есть, частные производные в равенстве (3) – это орты пространства-времени. Бросается в глаза интересная особенность четырехмерной скорости V4 в равенствах (3) и (4) – ее компонента времени оказывается константой:
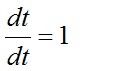
которая означает, что время в четырехмерном пространстве-времени может быть только линейной функцией! Это весьма важное ограничение на свойства пространства-времени. И вот почему. В процессе многолетнего (уже около 100 лет) теоретического осмысления этого пространства (включая различные инерциальные пространства с различными часами) в числе прочих свойств пространства утвердились преобразования Лоренца, пара которых для времени имеет вид [1, стр.523]:
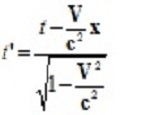и 
(6)
Вот что сообщает о них указанный справочник по физике:
«Преобразования Лоренца линейны и переходят при малых скоростях (при
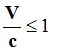в преобразования Галилея». Если отношение:
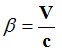(7)
полагать показателем релятивизма, то равенства (6) можно представить в виде функций трех переменных:
и 
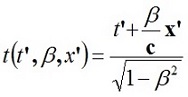(8)
Легко заметить, что эти функции зависят от произведения двух аргументов бета и икс (или икс-прим) из трех, что принципиально исключает линейность этих функций. То есть, утверждение о линейности преобразований Лоренца ошибочно. Это означает некорректность фундамента теории относительности. Именно некорректность фундамента вполне объясняет все недостатки и нестыковки теории, что, вообще говоря, не должно удивлять – задача была не из простых, да и сейчас ее нельзя полагать завершенной. Удивлять может только почти религиозная вера в авторитеты, с какой ученое сообщество приняло непроверенный постулат.
….
Литература
1. Яворский Б.М. и Детлаф А.А. – Справочник по физике для инженеров и студентов вузов. Издательство “Наука”. Главная редакция физико-математической литературы. М. 1974.
2. Океанов Е.Н. – Новая старая физика./ 2-е изд., перераб. и доп. – СПб: ЛИТЕО, 2017. – 192 с.
3. И.Н. Бронштейн и К.А. Семендяев – Справочник по математике для инженеров и учащихся ВТУЗОВ. Издание десятое, стереотипное. Издательство «Наука», Москва, 1964.