Измышленная Ньютоном формула силы гравитационного взаимодействия: F = gMm/r^2, где F сила взаимодействия, g — гравитационная постоянная, M и m — массы взаимодействующих тел, r — расстояние между ними лежит в основе современной как бы физики. Но, чем больше наблюдений, тем хуже эта формула отражает реальное взаимодействие объектов. Именно для исправления поведения глупой природы в соответствии с этой «умной» формулой и была измышлена «темная материя».
Израильский ученый Мордехай Мильгром (Mordehai Milgrom) усомнился в универсальности формул Ньютона, прежде всего формулы второго закона Ньютона F = ma, где F – сила, m – масса объекта, a – его ускорение. В случае движения звезд вокруг центра галактики, входящая в уравнение сила F – это сила притяжения. Так как нарушающие закон Ньютона звезды движутся с очень малыми ускорениями он предложил, что в системах, где ускорение падает ниже определенного критического значения a0, формулу F = ma надо заменить формулой F = ma2/a0. Формула Мильгрома корректно отражала движении галактик.
Конечно, подавляющее число ученых не восприняли идею Мильгрома, ведь его модифицированная ньютоновская динамика (МоНД) не соответствовала релятивистским теориям. (Были и попытки релятивистской модификации МоНД. Например это сделал Якоб Беркенштейн.)
Сторонникам МоНД долго не хватало фактических данных. Теория модифицированной ньютоновской динамики постулирует существование ряда эффектов, проявляющихся при ускорениях ниже критического ускорения a0. Оно составляет приблизительно 10-8 сантиметров на секунду в квадрате. (Ускорение свободного падения равно 9,81 метра на секунду в квадрате.) Заметить изменения движения объектов такого порядка да еще и на огромных расстояниях на современном уровне развития техники невозможно.
В марте 2018 года в журнале Nature была опубликована статья с результатами наблюдения неправильной карликовой галактики NGC1052–DF2, в которой отсутствовала темная материя. Ученые измерили скорость 10 объектов, находящихся в различных регионах галактики, и выяснили, что наблюдаемая дисперсия (разброс вокруг среднего значения) скоростей звезд NGC1052–DF2, почти в два раза ниже значения, рассчитанного в рамках MOND и равного приблизительно 20 километрам в секунду.
В новой работе физики оспорили выводы своих коллег, аргументируя тем, что NGC1052–DF2 не является изолированной галактикой и испытывает на себе гравитационное влияние со стороны своих соседей. Поблизости от нее, в 80 килопарсеках, находится яркая эллиптическая галактика NGC1052 (обе звездные системы удалены от Земли на 20 мегапарсеков). Таким образом, считают исследователи, при расчетах в рамках MOND необходимо учитывать ускорение звезд под влиянием внешних гравитационных сил.
Ученые рассчитали дисперсию скоростей (σ) для NGC1052–DF2, используя метод расчета результирующей гравитационной силы для N тел. Оказалось, что влияние NGC1052 уменьшает дисперсию для MOND до 15 километров в секунду, приближая ее к наблюдаемым значениям. При этом разница между теоретической и измеренной σ составила около двух стандартных отклонений и являлась статистически незначимой.
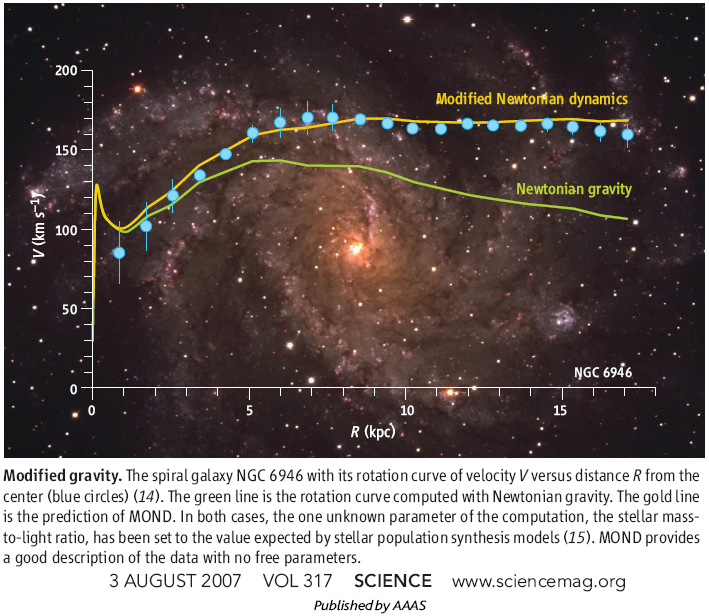
Сотрудник Мэрилендского университета (США) Стейси Макго (Stacy McGaugh) показал в своем наблюдении, что модифицированная ньютоновская динамика (МоНД) может без “тёмной материи” и более точно объяснить реальное вращение галактик. Чтобы понять её суть, достаточно взглянуть на кривую вращения обычной спиральной галактики — график, на котором показана зависимость орбитальной скорости звёзд и газа от расстояния до центра галактики. Наблюдения говорят о том, что скорость остаётся практически постоянной на очень большом интервале расстояний, а установленные физические законы требуют её уменьшения с удалением от центра; при добавлении «невидимой» массы тёмной материи всё встаёт на свои места.
МоНД предлагает совершенно иной способ решения проблемы — изменение традиционной динамики. В этой теории вводится новая константа с размерностью ускорения, а0, и устанавливается следующее: при высоких (намного превосходящих а0) ускорениях действует «старый» закон, а при низких — его модифицированный вариант. Другими словами, известную формулу F = m•a меняют на F = m•μ(а/а0)•a, где множитель μ(а/а0) принимает значение 1, если а много больше а0, и а/а0, если а меньше а0. Стоит заметить, что центростремительное ускорение, необходимое для сохранения звезды на орбите, составляет лишь около 10-10 м/с2 — гораздо ниже того, что испытывают планеты, обращающиеся вокруг Солнца (для Земли, к примеру, это ускорение равно 6•10-3 м/с2). Величина 10-10 м/с2 считается примерным значением константы а0.
Проверить предсказания МоНД довольно легко: нужно выяснить, соответствуют ли они эмпирическому соотношению Тулли — Фишера, которое связывает барионную массу галактик и амплитуду кривых вращения. При расчёте массы звёзд в галактике, однако, появляется заметная неопределённость, и ценность общего результата снижается. Оценка массы газа получается куда более точной.
В своей работе г-н Макго постарался снизить неопределённость результатов, ограничившись 47 галактиками, в которых масса газа превышает звёздную. Как оказалось, МоНД даёт прекрасное соответствие экспериментальным данным, причём подбирать параметры здесь нет необходимости. «Чертишь линию — и экспериментальные точки попадают прямо на неё, — говорит автор. — Всё просто и понятно».

Отобранные для исследования галактики лежат над красной прямой и отличаются тем, что масса газа в них превосходит звёздную. (Иллюстрация из журнала Physical Review Letters.)

Соотношение Тулли — Фишера для галактик с большой массой газа и предсказание МоНД (иллюстрация из журнала Physical Review Letters).
Наоборот, в случае теории “тёмной материи” для воспроизведения опытных данных требуется тонкая настройка. Действительно, галактики с одинаковой массой тёмной материи могут иметь разные звёздные массы, и ожидать чёткого соответствия было бы наивно.
Формула Мильгрома так же эвристична как и формулы Ньютона, то есть она тоже измышлена. Не даром Мильгром свою теорию назвал модифицированной Ньютоновской динамикой, то есть подправил Ньютона, а не отказался от любых неестественных формул. Мильгром не попытался найти формулу естественную, в которой масса не будет умножаться на массу, время на время, скорость на скорость и применяться тому подобные математические действия, никак не соотносимые с реальностями природы, но формула Мильгрома показала саму возможность искать естественную формулу, отказав в монополии формуле Ньютона!
