Можно даже сказать, что «закон всемирного тяготения – Ньютона» – это разновидность «2-го закона Ньютона».
Действительно, ведь формулу:

где, F- сила притяжения масс; – гравитационная постоянная; – массы тел; R – расстояние между центрами масс,
можно представить в виде.
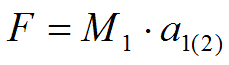
Где, – ускорение массы под действием массы .
Ускорение это определяется выражением:
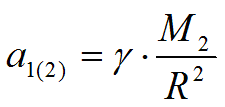
Как видно, формула это не что иное, как формула 2-го закона Ньютона.
Считается, что действие «закона всемирного тяготения» распространяется далеко за пределы Земли. Считается, что закон этот применяется для расчётов траекторий небесных тел и искусственных спутников Земли. Кроме того, принято считать, что закон этот выведен из астрономических наблюдений за движением планет, то есть, – имеет опытное происхождение.
Если бы это было так, то проверки области действия «2-го закона Ньютона» и «закона всемирного тяготения» не имели бы смысла, по крайней мере, в масштабах Солнечной системы. В действительности это далеко не так.
Дело в том, что астрономические наблюдения могут дать объективные данные лишь о геометрических размерах орбиты и о периоде обращения планеты. Зная эти данные, можно определить скорость движения тела по орбите и центростремительное ускорение.
В соответствии с этими объективными данными 3-й закон Кеплера устанавливает связь между периодами обращения тел и геометрическими размерами их орбит. На большее 3-й закон Кеплера не претендует. Он не даёт возможность определить силу взаимодействия тел, ибо для вывода формулы силы взаимодействия нет опытных данных. Опыты, в которых бы непосредственно определялась сила взаимодействия между небесными телами, не проводились и, вряд ли, когда-нибудь, будут проведены. Похоже, не проводились также опыты и по определению веса, то есть силы притяжения известной (пробной), массы, скажем, на поверхности Луны. Хотя эти последние опыты давно уже могли быть поставлены.
На сегодняшний день сила гравитационного взаимодействия между телами измерена только на поверхности Земли, что явно недостаточно для обоснования закона, претендующего на звание всемирного.
Тем не менее, «закон всемирного тяготения» претендует на определение силы взаимодействия тел и этим в корне отличается от 3-го закона Кеплера. Поэтому, «закон всемирного тяготения» не может быть, строго математически, выведен из 3-го закона Кеплера.
И действительно, из 3-го закона Кеплера можно вывести лишь выражение для определения центростремительного ускорения планет (выражение 15). А вот перемножение выражения
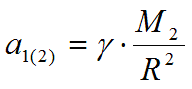
и массы тела – акт совершенно произвольный, не подтверждённый никакими опытами, и сделанный Ньютоном, очевидно, по аналогии со своим 2-м законом.
Так что, «закон всемирного тяготения», по существу, является гипотезой. А всеобщее мнение о том, что этот закон выполняется и применяется для расчётов в масштабах Солнечной системы – глубокое заблуждение. В практических расчётах по определению траекторий небесных тел и искусственных спутников применяется не сам «закон всемирного тяготения», выраженный формулой

и определяющий силу взаимодействия тел, а лишь его часть, то есть формула
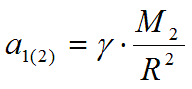
или её модификации.
Рассмотрим подробнее выражения для определения ускорения тел, в результате их гравитационного взаимодействия.
Если мы имеем два тела и , то, как уже отмечалось, тело сообщает телу
ускорение , равное
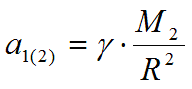
А тело сообщает телу ускорение , равное
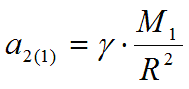
Где: и – абсолютные ускорения. То есть, ускорения относительно далёких, «неподвижных» звёзд.
Суммарное, то есть, относительное ускорение масс и (обозначим его ) будет равно их сумме. (17)
Подставляя в (17) выражения (15) и (16), получим
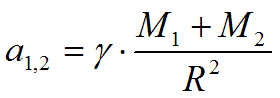
Это последнее выражение вполне можно назвать законом всемирного ускорения.
Если массы и значительно различаются, как например масса Солнца и масса какой-нибудь планеты, то есть, если >> , то можно не учитывать. И тогда, относительное ускорение будет, примерно, равно
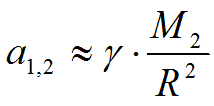
Используя выражение для центростремительного ускорения, выведенное ещё Гюйгенсом
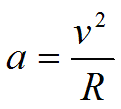
Где, – окружная скорость; R – радиус окружности
Для планет, обращающихся по круговым орбитам, можно показать, что выражения (15) и (19) сводятся к 3-му закону Кеплера
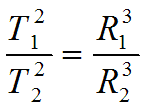
А выражение (16) сводится к 3-му уточнённому закону Кеплера
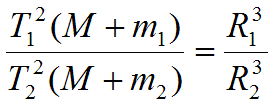
Где, М – масса, вокруг которой обращаются тела и .
Формула (21) выводится следующим образом.
Длина орбиты, радиуса , будет равна
Период обращения первой планеты , найдётся из выражения:
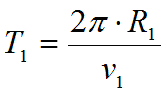
Где, – окружная скорость первой планеты.
Возведём в квадрат обе части этого выражения, получим:
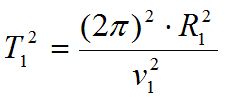
- определится из выражения центростремительного ускорения, для тела движущегося по окружности:

- Откуда,
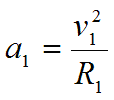
- Подставляя (26) в (24), получим:
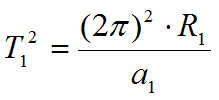
- Подставляя значение из формулы обратных квадратов (19), получим:
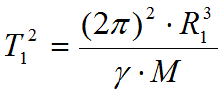
- Для планеты , обращающейся по радиусу , можно по аналогии записать:
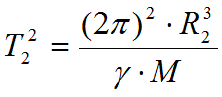
- Разделив почленно выражения (28) и (29) получим формулу 3-го закона Кеплера (21). Аналогично выводится формула 3-го уточнённого закона Кеплера (22)
Рассмотрение движения тел в гравитационном поле, анализ «2-го закона Ньютона», «3-го закона Кеплера» и «закона всемирного тяготения Ньютона», – позволяют сделать вывод об отсутствии экспериментального обоснования последнего.
Принимая также во внимание естественное соображение о том, что в более разряжённом гравитационном поле для ускорения тела потребуется меньшая сила, можно сформулировать очевидные следствия: - закон изменения ускорения свободного падения не может быть одновременно законом изменения силы или напряжённости гравитационного поля, какой либо гравитирующей массы;
- величина силы притяжения должна уменьшаться быстрее, чем величина ускорения свободного падения.
И если закон для силы гравитационного притяжения тел можно выразить через обратную степенную функцию, то показатель степени при R должен быть больше 2-х. И закон всемирного тяготения будет выглядеть так:
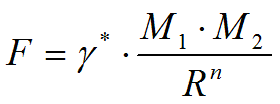
- Где, n >2; – гравитационная постоянная, значения которой мы пока не знаем. Ибо, значение гравитационной постоянной, которое определил Кавендиш, не верно уже только потому, что при её расчёте пользовались формулой обратных квадратов. Кроме того, опыты по определению силы гравитационного притяжения пробных тел проводились на поверхности Земли, при воздействии сильного внешнего гравитационного поля Земли, влияние которого на результаты эксперимента не было учтено. Выводы к главе
«Закон всемирного тяготения» Ньютона – представляет собой разновидность 2-го закона Ньютона.
«Закон всемирного тяготения» не имеет опытного обоснования и не может быть, строго математически, выведен из 3-го закона Кеплера. Третьему закону Кеплера соответствует лишь один из сомножителей в формуле «закона всемирного тяготения», а именно выражение центростремительного ускорения взаимодействующих тел.
Ньютон, без всяких на то оснований, приравнял силу притяжения масс произведению одной из масс на её ускорение свободного падения. В построении этой формулы прослеживается явная аналогия с формулой 2-го закона Ньютона. В этом и заключается основная ошибка Ньютона. Он, по сути, без проведения экспериментов, расширил действие 2-го закона на всю Вселенную.
Значение гравитационной постоянной, входящей в формулу «Закона всемирного тяготения, также требует уточнения.
«Закон всемирного тяготения» – это не более чем гипотеза.
Гужеля Юрий Александрович
