Физики из Австрии и США провели вариант эксперимента Фарадея вперыве показавшего, что при распространении линейно-поляризованного света через оптически неактивное вещество, находящееся в магнитном поле, наблюдается вращение плоскости поляризации.
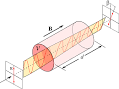
В том варианте этого эксперимента, что сделали физики из Австрии и США свет вращали магнитным полем в тонких пленках. Оказалось, что скачок угла поляризации в точности равен постоянной тонкой структуры. Исследование опубликовано в Applied Physics Letters.
Постоянная тонкой структуры возникла в физике благодаря увеличению точности, с которой экспериментаторы научились определять энергии атомных уровней. Ее ввел Арнольд Зоммерфельд в 1916 году как параметр, определяющий то, насколько сильно расщепляются уровни в тонкой структуре.
Помимо спектроскопического способа определения постоянной тонкой структуры физики используют астрофизические данные, но в обоих случаях константа получается как результат математической комбинации измеренных параметров той или иной размерности.
И все же экспериментаторы нашли прямой доступ к постоянной тонкой структуры. Оказалось, сто поворот плоскости поляризации может происходить лишь на целое число, умноженное на угол, в точности равный постоянной тонкой структуры. Проблема в том, что без дополнительных усилий квантовый эффект Холла возникает только при слишком низких частотах, а сильное магнитное поле, нужное, чтобы его увидеть, размывает квантование. Чтобы обойтись без сильных магнитных полей, Алексей Шуваев (Alexey Shuvaev) из Венского технологического университета и его коллеги из Австрии и США обратились к аномальному эффекту Холла. В отличие от своей нормальной версии, аномальный эффект возникает в материалах, которые способны поддерживать достаточно большую намагниченность в отсутствие магнитного поля, и связан со спиновыми свойствам носителей зарядов. Его квантовая версия впервые была обнаружена лишь в 2013 году.
Физики проводили опыты с монокристаллами (Cr0,12Bi0,26Sb0,62)2Te3, выращенными методом молекулярно лучевой эпитаксии на подложке арсенида галлия. Образцы имели форму, близкую к шестиугольной с характерным размером около 10 миллиметров и толщиной 6 нанометров. К углам авторы присоединяли индиевые контакты для измерения холловского сопротивления.
Суть опыта заключалась в прохождении через образец терагерцового излучения и измерения пропускания в схеме параллельных и скрещенных поляризаторов. В этом случае угол фарадеевского вращения определяется через арктангенс этих двух величин. Поскольку каждая пленка представляет собой идеальную пластинку, в некотором диапазоне частот пропускание демонстрирует характерную интерференцию Фабри — Перо. Основной результат авторы получили на частоте одного из максимумов — 188 гигагерцах.
Ученые строили зависимость обеих пропусканий и холловского сопротивления от приложенного магнитного поля при различных температурах. Сильнее всего эффект квантования проявил себя при гелиевых температурах (а именно при 1,8 кельвин). Так, в отсутствие магнитного поля вращение поляризации равнялось нулю, но по достижению нескольких сотен миллитесл оно достигало значения, примерно равного 1/137 радиан. При этом возникал характерный гистерезис этого угла при изменении направления магнитного поля, связанный с гистерезисом намагниченности.

Угол вращения поляризации в зависимости от магнитного поля при различных углах. Штриховая линия соответствует величине, в точности равной постоянной тонкой структуры.
Alexey Shuvaev et al. / Applied Physics Letters, 2022
Примечательно, что скачок холловского сопротивления не превышал шести килоом при самых холодных условиях, что все еще меньше, чем фундаментальный квант сопротивления, равный 26 килоом. Это свидетельствует о различии в механизмах оптического и статического эффектов Холла. В то время как последний основан на одномерных проводящих каналах на краях образца, терагерцовое излучение не задействует этот механизм, поскольку физики фокусировали его в пятно диаметром пять миллиметров в середине образца.
