Статья Менде приведена полностью. Она интересна практическим опровержением постулатов Эйнштейна. Но теория Менде, как бы объясняющая полученный эффект это такие же измышления, как и измышления Эйнштейна. Точнее сказать измышления релятивистов и эфиристов равноценны в игнорировании реальности. Сергей Сергеев.
Интерферометр Менде

Федор Менде
Разработан интерферометр нового типа, использующий принцип механического деления луча лазера. С его помощью экспериментально обнаружено постоянство во времени длины волны лазерного луча, которая не зависит от скорости движущихся по гармоническому закону генератора или зеркала. Сочетание данного нового эффекта с известным эффектом Доплера свидетельствует об имеющем место в данном случае классическом сложении скорости света со скоростью его источника, нарушающем принцип инвариантности скорости света теории относительности. Благодаря обнаруженному эффекту, использование разработанного интерферометра в пассивной радиолокации открывает новые перспективы её развития.
Ключевые слова: специальная теория относительности, интерференция, лазер, интерферометр Майкельсона, эффект Доплера, закон Снелиуса, радиолокация.
1. Введение
Интерферометр американского физика Альберта Абрахама Майкельсона позволил решить ряд важных научных и прикладных задач, в частности, высокоточного измерения скорости света. Однако при измерении зависимости скорости света от движения системы отсчёта Майкельсон и Морли допустили критическую ошибку. До конца жизни Майкельсон считал свет колебаниями особой упругой среды (светоносного эфира), но результаты эксперимента [1] и его более позднего эксперимента, использующего в качестве источника излучения свет звезды, противоречили эфирной концепции. Измеренная скорость света не зависела от скорости Земли относительно звезды и равнялась ранее измеренному им значению. На этой эмпирической основе постулирован принцип инвариантности скорости света в специальной теории относительности (СТО), которую Майкельсон не признал до конца жизни.
Для выявления ошибки Майкельсона рассмотрим принцип работы его интерферометра [2] по схеме на рис. 1.
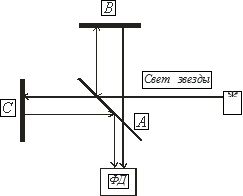
Рис. 1. Схема интерферометра Майкельсона
Луч звезды, отраженный от делительного зеркала А, попадает сначала на отражающее зеркало В, а потом на фотодетектор. Так как зеркало В покоится в инерциальной системе отсчёта (ИСО) интерферометра, то отражённый от него свет является светом от неподвижного (в данной ИСО) источника вне зависимости от особенностей распространения света до отражения. Это означает, что, какая бы не была скорость волны, пришедшей от звезды, её скорость после отражения от зеркала В будет равна скорости света в ИСО интерферометра.
Вторая часть световой волны звезды, проходя через делительное зеркало А, также попадает на отражательное зеркало С. После отражения волна также представляет собой свет от неподвижного источника. Аналогичная ситуация имеет место с волной, прошедшей делительное зеркало с отражающим покрытием, нанесённым на прозрачную стеклянную пластинку. Поскольку диэлектрическая проницаемость стекла отлична от воздуха, траектория луча зависит от показателя преломления стекла (рис. 2).

Рис. 2. Распространение луча света через стеклянную пластинку
Луч света падает на стеклянную пластинку со стороны полупрозрачного покрытия и далее, преломляясь дважды, выходит из неё в том же направлении. При обратном движении луча его траектория остаётся неизменной. При этом луч движется в соответствии с законом Снелиуса [2], резко меняя своё направление после входа и выхода из пластинки. Но такое преломление луча связано с тем, что электрические поля волны заставляют колебаться связанные заряды в диэлектрике, переизлучая эти поля. Вне зависимости от особенностей распространения света до входа в пластинку, после выхода из неё он будет светом от неподвижного источника.
Ошибка Майкельсона состояла в том, что при помощи его интерферометра можно было бы измерить скорость света до его попадания на делительное зеркало только в том случае, если скорость света остаётся неизменной после прохождения через рассмотренные зеркала. В рамках концепции светоносного эфира, которой придерживался Майкельсон, это предположение вполне оправдано, так как, согласно неё, скорость света неизменна относительно эфира. Но вне рамок эфирной концепции следует различать скорость света от неподвижного источника и скорость света от подвижного источника.
Впоследствии были изобретены такие модификации интерферометра Майкельсона, как интерферометр Жамена, Рождественского, Фабри-Перо и другие приборы с многократно разделёнными световыми пучками [2]. Но везде для деления, разделения и отражения световых лучей используются полупрозрачные или отражающие слои металлов, нанесённые на стеклянные пластинки, или границы раздела между диэлектриками с различной диэлектрической проницаемостью. Поэтому все указанные интерферометры страдают тем же недостатком, что и интерферометр Майкельсона. Поэтому при их помощи нельзя определить скорость приходящей извне волны. Поэтому необходима разработка интерферометра принципиально нового типа, лишенного этих недостатков.
Но есть ещё одно обстоятельство, которое следует учитывать при постановке таких экспериментов.
Явление фазовой аберрации света заключается в том, что при астрономических наблюдениях такая аберрация приводит к изменению наблюдаемого положения звёзд на небесной сфере вследствие изменения направления скорости движения Земли. В астрономии используют систему отсчёта, связанную с Солнечной системой, поскольку её с высокой точностью можно считать инерциальной. Звёздные атласы составлены именно в ней. Суточная аберрация мала, и даже угол годичной аберрации не велик; наибольшая его величина, при том условии, что движение Земли перпендикулярно направлению луча, составляет всего около 20,5 секунды. Звезда, находящаяся в полюсе эклиптики, лучи которой перпендикулярны плоскости земной орбиты в системе отсчёта Солнца, будет в течение всего года наблюдаться отстоящей от своего истинного положения на 20,5 секунды, то есть описывать окружность диаметром 41 секунда. Этот кажущийся путь для прочих звёзд уже будет представлять не окружность, а эллипс. Большая полуось этого эллипса равна 20,5″, а малая полуось равна 20,5″sinβ, где β – эклиптическая широта наблюдаемого небесного светила. Если звезда находится на самой эклиптике, то её годовое движение, вследствие световой аберрации, представится видимым отрезком прямой линии, являющимся дугой эклиптики на небесной сфере, и по этому отрезку звезда идёт то в одну сторону, то в другую. Но аберрация света прямым образом указывает на сложение скорости света со скоростью Земли. Рассмотрим этот вопрос подробнее.
На рис. 3 изображена схема аберрации света звезды, когда она находится в полюсе эклиптики, и её лучи перпендикулярны плоскости земной орбиты. В системе отсчёта звезды её луч двигается со скоростью света вертикально по отношению к земной поверхности. Если Земля двигается, как показано на рисунке вправо со скоростью , то сложение вектора скорости луча звезды и скорости Земли в системе отсчёта Земли происходит по правилу сложения векторов, как показано на рисунке. Это означает, что суммарная скорость луча будет определяться в соответствии с соотношением . Эта скорость больше скорости света .
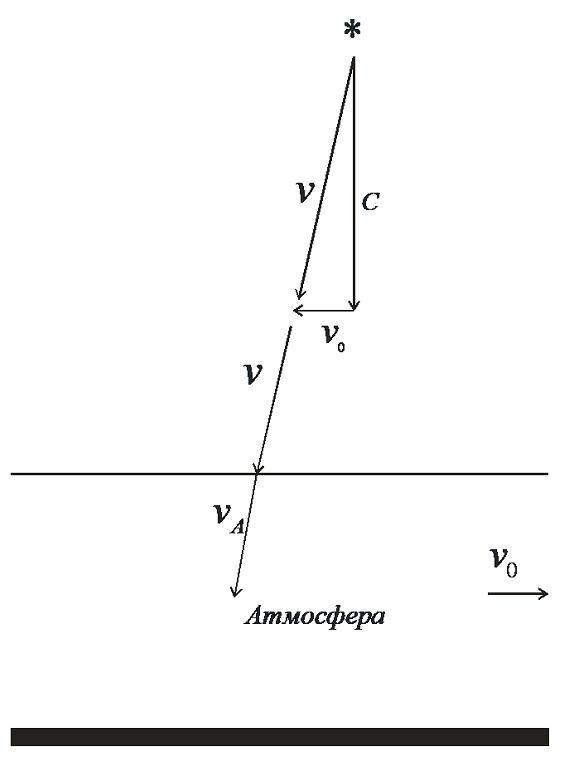
Рис. 3. Схема аберрации света звезды
В данном случае суммарный вектор скорости луча уже не вертикален земной поверхности, а его угол наклона равен углу аберрации, тангенс которого определяется, как отношению скорости Земли к скорости света. Продолжая своё движение в указанном направлении, луч достигает атмосферы (в данном случае считается, что у атмосферы резкая граница с вакуумом космоса). Но воздух атмосферы имеет диэлектрическую проницаемость большую, чем диэлектрическая проницаемость вакуума, поэтому на границе с атмосферой луч испытывает преломление в соответствии с законом Снелиуса и изменяет свою скорость и направление. До попадания в атмосферу скорость луча была больше, чем скорость света в воздухе, но при попадании в атмосферу он изменяет свою скорость таким образом, чтобы она соответствовала скорости света в воздухе.
Поперечный эффект Доплера, который обсуждается достаточно давно, до сих пор не нашел своего уверенного экспериментального подтверждения. Для наблюдения звезды из движущейся ИСО необходимо наклонять телескоп по ходу движения на угол, определяемый соотношением
Звезда, наблюдаемая в зените, в действительности находится несколько позади по направлению движения. Но это будет означать, что такая звезда по отношению к наблюдателю имеет радиальную составляющую скорости, определяемую соотношением
Для малых углов , , и доплеровский сдвиг частоты равен
Данный результат численно совпадает с результатами СТО, но принципиально отличается тем, что в СТО поперечный эффект Доплера считается реальным, а в данном случае это только кажущийся эффект.
В то же время, если Земля и звезда сближаются или удаляются по направлению луча, то происходит простое сложение векторов, при котором скорость луча может быть как больше, так и меньше скорости света. В этом случае имеет место эффект Доплера, при котором частота волны в системе наблюдения Земли получает доплеровскую добавку, знак которой зависит от относительной скорости Земли и звезды. Этот вопрос мы обсудим ниже.
Известны многочисленные попытки измерения скорости света, излучаемого движущимися источниками. Наиболее характерные из них приведены в работах [3-11], но все эти эксперименты давали один и тот же результат, подтверждающий постулат теории относительности об инвариантности скорости света. Но другого результата и не могло быть, так как существующие интерферометры, используемые в экспериментах, для этих целей не пригодны. Более того, все указанные эксперименты следует проводить в высоком вакууме, поскольку при попадании в материальную среду (в данном случае воздух) электромагнитная волна приобретает скорость, которая определяется диэлектрической проницаемостью среды.
В статье предлагается новый тип интерферометра, лишенного выявленного недостатка. В основу его работы положен принцип расщепления луча.
2. Интерферометр с механическим делением луча лазера
Схема интерферометра с механическим делением луча лазера показана на рис. 4.
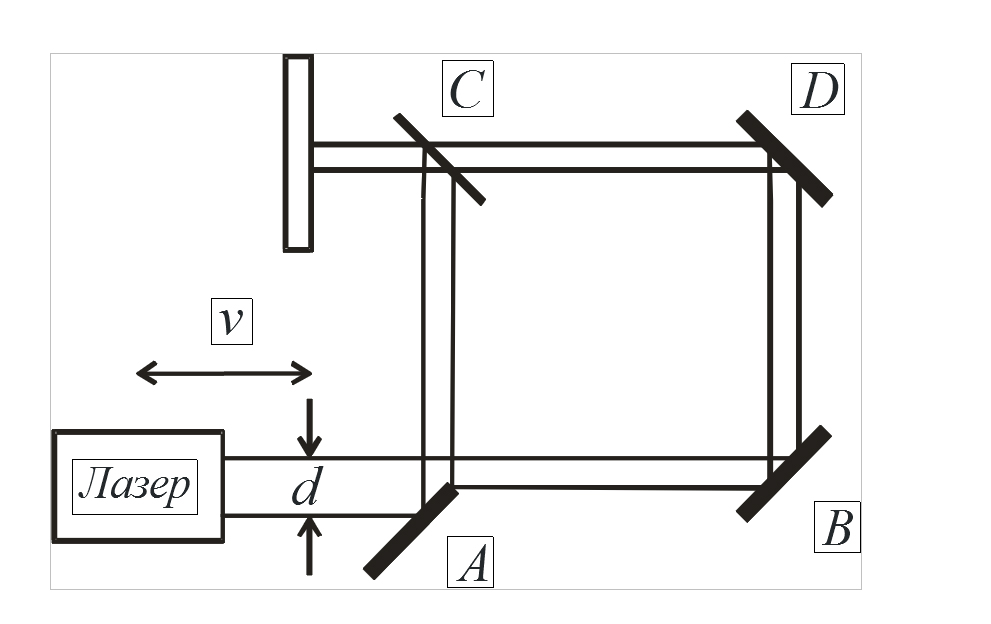
Рис. 4. Схема интерферометра с механическим делением луча лазера
Луч лазера, диаметр которого равен d, частично перекрывает отражающее зеркало А. Это зеркало расположено так, что часть луча оно отражает в нормальном направлении по отношению к первичному направлению движения луча. Вторая часть луча продолжает двигаться в прежнем направлении с прежней скоростью и, попадая на отражающее зеркало В, отражается в вертикальном направлении по отношению к первоначальному направлению движения. Далее лучи, пройдя пути, указанные на схеме, где D – отражающее зеркало, а зеркало C – делительное, попадают на экран, где и воспроизводится картина их интерференции. В рассмотренной схеме лазер, который является источником излучения, может быть неподвижным или двигаться с заданной скоростью. На месте лазера также может находиться зеркало, которое отражает луч неподвижного лазера, при этом зеркало также может быть неподвижным или двигаться по заданному закону. Этот случай эквивалентен рассмотренному с той лишь разницей, что в качестве луча, испускаемого движущимся лазером, используется луч, отраженный от движущегося отражательного зеркала. Преимуществом интерферометра с механическим делением луча является то, что в нём не используются делительные зеркала, а деление луча в заданной пропорции производится методом его механического перекрытия.
Схема интерферометра с механическим делением луча, в котором используется неподвижный лазер, луч которого отражается от неподвижного или движущегося зеркала, изображена на рис. 5. На этой схеме луч лазера имеет диаметр, который равен расстоянию между линиями, выходящими из лазера.

Рис. 5. Схема интерферометра с отражательным зеркалом
Опишем параметры исследуемого интерферометра и способ его настройки.
Интерферометр смонтирован на монтажной плите размером 75х300х1200 мм и имеет следующие параметры: расстояние между наконечником лазера и зеркалом В – 200 мм, расстояние между зеркалами А и В, а также D и С 250 мм, расстояние между зеркалами А и D, а также В и С – 200 мм. Расстояние от наконечника лазера до отражающего зеркала -1400 мм.
В интерферометре в качестве лазера используется лазер с зелёным лучом Green Laser Pointer с длиной волны 532 нм мощностью 5 мВт. Диаметр его луча составляет 1.1 мм. Лазерный луч выходит из наконечника. На этот наконечник с внешней стороны одет отражающий экран, в котором имеется отверстие для прохождения луча диаметром около 2 мм. Вначале отражающие зеркала А и В устанавливаются таким образом, чтобы они не мешали прохождению прямого и отраженного луча лазера. При этом положение лазера и отражающего зеркала устанавливается так, чтобы прямой и отраженный луч и поверхность платформы были параллельны.
В интерферометре имеется вибратор, осуществляющий колебательное движение отражающего зеркала. Для исключения влияния вибратора на работу интерферометра он установлен на отдельной монтажной плите размером 75х300х650 мм. Эта плита устанавливается на отдельном столе. Кроме этого, вибратор находится в коробе, внутри которого имеется футеровка из поролона, а луч на отражающее зеркало попадает через отверстие в коробе. Это сделано для того, чтобы звуковая волна, генерируемая вибратором, не влияла на работу интерферометра. Вибратор обеспечивает гармоническое колебание отражающего зеркала с частотой 50 Гц. Амплитуда колебаний зеркала может регулироваться от нуля до 5 мм.
Настройка интерферометра производится в следующем порядке. Луч лазера наводится на неподвижное отражающее зеркало, и это зеркало устанавливается таким образом, чтобы отраженный луч попадал на экран на наконечнике лазера. При этом расстояние от отражения луча на экране до отверстия в нём должно составлять порядка 2-4 мм в параллельном плоскости платформы направлении. Затем зеркала А и В устанавливаются под углом 45 градусов по отношению к направлению отраженного луча. Далее зеркало В выдвигается по направлению к лучу таким образом, чтобы оно полностью перекрыло отраженный луч, но не перекрывало прямой. После этого выдвигается зеркало А до тех пор, пока интенсивности лучей, отраженных от зеркал A и D, будут равны. Далее, юстируя зеркала D и С, следует добиться сведения лучей на экране, расположенного по ходу лучей. Для увеличения интерференционной картинки используется объектив, установленный по ходу лучей (на схеме не показан). Затем следует включить вибрацию отражающего зеркала и наблюдать поведение интерференционной картинки на экране. Если необходимо вывести сигнал, даваемый сведенными лучами на осциллограф, следует использовать фотодетектор.
Авторы по доступной им литературе не обнаружили каких-либо аналогов описанного выше интерферометра и поэтому присваивают этой созданной ими конструкции название интерферометра Менде-Дубровина.
3. Экспериментальная проверка справедливости преобразований Лоренца и принципа инвариантности скорости света
Созданная Эйнштейном и господствующая в физике уже более ста лет СТО [12, 13] использует преобразования Лоренца, основанные на постулируемом в ней принципе инвариантности скорости света, который вызывает критику со стороны многих учёных.
Пусть излучение в прозрачной среде с коэффициентом преломления имеет в ИСО , неподвижной относительно источника, частоту и волновое число . Тогда, если ИСО движется по отношению к ИСО , неподвижной относительно среды, со скоростью , то, согласно СТО, частота и волновое число излучения в ИСО определяются следующими преобразованиями, вытекающими из преобразований Лоренца:
, (3.1)
. (3.2)
Одновременное изменение частоты и волнового числа при переходе из ИСО в ИСО происходит таким образом, что отношение частоты к волновому числу в обеих ИСО остаётся равным скорости света в среде . Какие бы причины ни привели к изменению частоты, всё равно выполняются соотношения (3.1), (3.2). Этих причин может быть две: изменение частоты генерации неподвижного генератора и эффект Доплера от движущегося генератора. С точки зрения СТО найти истинную причину невозможно.
Если приёмник движется со скоростью относительно среды в направлении источника, то скорость волны относительно приёмника получается релятивистским сложением этой скорости со скоростью волны относительно среды:
,
где – – коэффициент увлечения. Данное приближение выполняется в первом порядке по . В СТО частичное увлечение света средой, приближённо описываемое коэффициентом , есть кажущийся эффект, обусловленный релятивистским сложением скоростей. Реальное же (физическое) увлечение света средой является полным. Это проявляется в том, что скорость света в среде зависит от скорости приёмника относительно среды, но не зависит от скорости источника относительно среды. Данное приближённое равенство подтверждается опытом Физо. Но это не означает, что опыт Физо доказывает СТО, так как он имеет и классическое объяснение (в рамках преобразований Галилея).
Классическое объяснение опыта Физо оставляет справедливым данное приближённое равенство лишь в случае источника, покоящегося относительно приёмника, но меняет его интерпретацию. Физическое увлечение света средой уже является частичным, точно описываемым коэффициентом . Это проявляется в том, что скорость света в среде зависит не только от скорости приёмника относительно среды, но и от скорости источника относительно среды. Если приёмник покоится относительно среды, а источник движется строго навстречу приёмнику со скоростью , то скорость волны относительно них равна . Эта скорость меньше результата соответствующего классического сложения скоростей на величину . Если же источник движется в направлении, строго противоположном приёмнику, то величина заменяется на величину , и скорость волны оказывается равной величине .
Рассмотрение эффекта Доплера начнём с его классической теории.
Пусть источник излучения плоской поперечной ЭМ волны покоится в выбранной ИСО. Тогда, если волна распространяется по пространственной оси , и в начале координат её электрическое поле изменяется по закону
,
то это же значение поля будет наблюдаться в любой точке наблюдения с запаздыванием , где – фазовая скорость волны. В этом случае зависимость электрического поля от координаты и времени примет вид
.
Текущие значения фазы в точках наблюдения и соответственно равны
, (3.3)
. (3.4)
Разность фаз между указанными точками при этом составит
,
где – расстояние между точками наблюдения, – волновое число.
Пусть теперь генератор движется в выбранной ИСО. Тогда, если в точке наблюдения фаза волны опять определяется соотношением (3.3), то в точке наблюдения фаза волны по-прежнему будет определяться соотношением (3.4). Если же по каким-либо причинам частота приходящей волны станет равной , то для фазы волны будут выполняться те же соотношения (3.3) и (3.4) с новым значением частоты.
Если генератор волны движется с постоянной скоростью , то фазы волны в точках и будут изменяться по закону
, (3.5)
. (3.6)
Разность фаз между точками наблюдения при этом составит
. (3.7)
где – длина волны.
Разность фаз (3.7) от скорости генератора не зависит. Это связано с тем, что скорость волны в выбранной системе отсчёта постоянна. Частота же сигнала в указанных точках будет изменяться по закону
, (3.8)
. (3.9)
Видно, что в обеих точках наблюдения частота получила одинаковую, не зависящую от расстояния до генератора, доплеровскую добавку
. (3.10)
Если разность фаз (3.7) неизменна при движении генератора, то неизменна и длина волны. В этом случае изменение частоты в точках наблюдения может быть связано только с изменением фазовой скорости волны в выбранной ИСО. Это изменение можно определить из соотношения
, (3.11)
откуда получаем
.
Это означает классическое сложение скорости света и скорости генератора, а значит скорость волны в выбранной ИСО может быть как больше, так и меньше стандартной скорости света в среде, в том числе и в вакууме, что противоречит СТО.
Далее рассмотрим релятивистскую теорию эффекта Доплера.
Согласно (3.1), (3.2), частота меняется одновременно с волновым числом, а значит и с разностью фаз между точками наблюдения. Эта разность фаз зависит и от скорости генератора, и от расстояния между этими точками. Частоте (3.8) или (3.9) соответствует волновое число
,
поэтому разность фаз между точками наблюдения в СТО изменяется по закону
. (3.12)
Из соотношения (3.12) следует, что разность фаз между точками наблюдения будет зависеть от расстояния между этим точками и от скорости генератора. В классическом же случае, как следует из соотношения (3.7), разность фаз между точками наблюдения от скорости генератора не зависит.
Поэтому задачей предлагаемого эксперимента является измерение разности фаз между точками наблюдения для случая движущегося генератора. Если окажется, что разность фаз не зависит от скорости движения генератора, то это будет означать, что СТО, преобразования Лоренца и принцип инвариантности скорости света не верны.
Рассмотрим в рамках СТО случай, когда генератор колеблется вдоль оси по гармоническому закону с частотой :
,
где – начальное положение генератора, – амплитуда его колебаний.
Тогда скорость колебаний генератора будет определяться соотношением
,
где – амплитуда скорости.
В этом случае доплеровская добавка к частоте в обеих точках наблюдения будет изменяться по закону
,
а добавка к волновому числу определится соотношением
.
Разность фаз между точками наблюдения, вызванная этой добавкой, составит
. (3.13)
Этой зависимости разности фаз от времени соответствует частотно модулированный сигнал, частота которого будет меняться по закону
, (3.14)
т.е. в рамках СТО будет получен частотно-модулированный сигнал, частота которого изменяется по гармоничному закону и амплитуда девиации частоты которого равна
.
Так как в СТО , то последнее равенство можно записать в виде
.
В любой материальной среде величина всегда больше, чем в вакууме, в раз, но в воздухе этим различием можно пренебречь.
Рассчитаем ожидаемые параметры сигнала, поступающего с фотодетектора, для рассмотренного случая. Для этого используем параметры интерферометра, описанного выше, на котором проводились исследования. Расстояния между зеркалами А и В составляло 250 мм, частота колебаний вибратора – 50 Гц, амплитуда колебаний зеркала равна 5 мм. При этих параметрах (в случае состоятельности СТО) амплитуда девиации частоты частотно-модулированного сигнала, который должен быть выделен на фотодетекторе, составит около 180 Гц. Такой сигнал легко поддаётся обнаружению и измерению.
Однако, при проведении эксперимента по схеме, представленной на рис. 5, интерференционная картинка не изменялась, как в случае неподвижного отражающего зеркала, так и в случае его колебаний, и интерференционные полосы остались на своих местах, картинка лишь растягивалась по вертикали примерно на 50%. Это связано с тем, что ось колебаний отражающего зеркала слегка наклонена по отношению к отраженному лучу лазера. Особо чётко различались интерференционные полосы, когда они располагались вертикально. При включении вибратора они только удлинялись. Поскольку интерференционные полосы при включении вибрации зеркала не меняли своего положения и не двигались, то и сигнал на фотодетекторе отсутствовал. Поскольку в процессе эксперимента не был обнаружен частотно модулированный сигнала, снимаемый с фотодетектора, это означает, что связь между частотой и волновым числом, определяемая соотношениями (3.1) и (3.2), не выполняются, что противоречит СТО. Экспериментальные результаты указывают также на то, что в данном случае выполняются преобразования Галилея, и скорость источника излучения складывается со скоростью света.
Рассмотрим этот вопрос для вакуума на примере ленточной пилы (рис. 6).

Рис. 6. Работа ленточной пилы
Из станка, обозначенного квадратом, со скоростью выходит ленточная пила, зубья которой нарезаны в виде синусоиды. Если расстояние между зубьями равно , то частота выхода зубьев из станка равна , где – скорость движения ленты пилы. Между двумя линиями наблюдения, расположенными на расстоянии , при этом помещается количество зубьев, равное , а скорость движения зубьев через линии наблюдения равна . Предположим, что станок начинает двигаться в сторону линий наблюдения со скоростью . Вместе с ним будет двигаться и движущаяся пила. При этом скорость движения зубьев относительно линий наблюдения увеличится и станет равной , но количество зубьев пилы между линиями при этом останется прежним. Частота прохождения зубьев через линии наблюдения также увеличится и станет равной . Допплеровская добавка к частоте прохождения зубьев через линии при этом составит . Можно рассмотреть и другой случай, когда станок остаётся неподвижным, а обе линии наблюдения двигаются в сторону станка со скоростью . Ситуация будет та же, что и при движении станка в сторону линий. Следовательно, количество зубьев, находящихся между линиями наблюдения не зависит от скорости станка или наблюдателей.
Подобная ситуация имеет место на участке АВ в интерферометре, поскольку оказались справедливы преобразования Галилея. Только вместо зубьев пилы мы имеем дело с электромагнитной волной, генерируемой неподвижным или движущимся генератором.
При движении генератора в воздухе со скоростью в сторону отражающих зеркал на всём участке АВ луч движется со скоростью , в то время, как в остальных плечах интерферометра он движется со скоростью . Так как в процессе эксперимента обнаружено, что разность фаз на участке АВ не зависит от скорости генератора, на этом участке длина волны также не зависит от скорости генератора. А это означает, что доплеровская частота, фиксируемая в точках наблюдения, которая зависит от скорости генератора, не связана с длиной волны на этом участке.
Такой факт противоречит преобразованиям Лоренца и принципу инвариантности скорости света, указывая на то, что скорость источника излучения складывается со скоростью света по классическому правилу.
Но была ли достигнута в проведённом эксперименте сверхсветовая (больше константы скорости света в вакууме) скорость распространения волны в ИСО интерферометра? Нет, не была, так как эксперимент проводился в атмосферном воздухе. Для превышения скоростью волны константы скорость источника (генератора или зеркала) навстречу интерферометру и показатель преломления должны быть связаны неравенством
.
Выражая из этого неравенства величину , имеем:
.
Для воздуха в нормальных условиях (=0,0003) получаем астрономическую скорость источника >90 км/с. Но можно добиться снижения этой скорости за счёт снижения величины , достигаемого заменой воздуха вакуумом. При заданной величине требование на величину имеет вид:
.
По крайней мере, зеркала А и В, промежуток между ними и движущимся зеркалом, и само зеркало должны находится в вакуумной камере.
Положим, что величина пропорциональна давлению остаточных газов в камере. Если принять скорость зеркала равной 1 м/с, то достаточно уменьшить давление в камере на шесть порядков, чтобы с десятикратным запасом выполнить поставленное условие. Такой вакуум считается низким, и его достижение – не проблема при современном уровне вакуумной техники.
4. Использование интерферометра с механическим делением луча для целей пассивной радиолокации
Предлагаемый интерферометр может быть использован для целей пассивной радиолокации. Для определения скорости движущегося генератора следует определить длину волны на участке АВ. Для этого одно из зеркал нужно сделать подвижным и его перемещение сопоставить с количеством полос, соответствующих этому перемещению. По измеренному значению длины волны следует определить частоту движущегося генератора . Затем нужно измерить частоту в одной из точек наблюдения. При этом скорость движущегося генератора определится из соотношения
. (3.15)
Движущийся генератор таким способом легко отличить от неподвижного, частота которого изменяется. Для неподвижного генератора длина волны , измеренная между точками наблюдения, и частота , измеренная в точках наблюдения, будут связаны соотношением
Общий вид интерферометра показан на рис. 7.

Рис. 7. Общий вид интерферометра
Интерференционная картинка, полученная на интерферометре, представлена на рис. 8.

Рис. 8. Интерференционная картинка
5. Заключение
Эмпирической основой принципа инвариантности скорости света СТО принято считать класс физических экспериментов, использующих интерферометр Майкельсона и называемых опытами Майкельсона. Однако до последнего времени оставался открытым вопрос о том, объясняются ли результаты этих опытов указанным принципом или же какими-то другими причинами. Это обусловливало актуальность совершенствования средств и методов соответствующих проверок в направлении повышения чистоты эксперимента, то есть устранения других возможных причин объяснения.
С этой целью авторами разработан новый тип интерферометра с механическим делением луча лазера и предложен метод проверки СТО с помощью такого интерферометра. Если бы вслед за опытами Майкельсона предложенный метод опять подтвердил СТО, то можно было бы и дальше совершенствовать средства и методы проверок, но при этом следовало бы признать ещё большую степень экспериментального подтверждения данной теории. Однако результаты проведённого эксперимента показали, что скорость света от движущегося генератора получается классическим сложением скорости света относительно генератора со скоростью его движения. Следовательно, СТО не верна, в чём может убедиться любая лаборатория мира, повторив наш простой эксперимент. А ведь это означает начало заката целой эры в истории физики – эры, упразднившей для высоких скоростей движения преобразования Галилея при переходе из одной ИСО в другую и заменившей их преобразованиями Лоренца. Проведённый эксперимент показал несостоятельность такой замены.
В работе также показано, какие ошибки совершали ранее экспериментаторы, пытаясь доказать состоятельность постулата СТО об инвариантности скорости света. Намечен путь преодоления указанных ошибок с помощью разработанного интерферометра.
Новой идеологии электродинамики и всей физики, предполагающей фундаментальную роль преобразований Галилея, посвящена монография авторов статьи [14], где в рамках представлений о не инвариантности теоремы Гаусса для электрического поля движущегося заряда вводится новое понятие скалярно-векторного потенциала, а также предлагаются новые преобразования полей, связанные с преобразованиями координат Галилея. Ещё Максвелл использовал преобразования Галилея при построении электродинамики. Однако в то время ещё не была выяснена фундаментальная роль преобразований Галилея, как связующего начала между пространством и временем, и эти преобразования пренебрежительно ставились как бы особняком по отношению к «настоящим» преобразованиям отдельно пространства и отдельно времени. А ведь именно фундаментальная роль преобразований Галилея предопределяет существование эффектов, которые принято называть релятивистскими, но которые, как оказалось, не имеют к преобразованиям Лоренца никакого отношения.
Авторы надеются, что появление их монографии [14] в совокупности с представленными экспериментальными результатами побудят исследователей к давно назревавшему революционному пересмотру фундаментальных физических представлений.
Важное техническое приложение результата данной работы относится к пассивной радиолокации. В СТО принципиально невозможно отличить изменение частоты, создаваемое неподвижным генератором, от такого же изменения частоты, вызванного эффектом Доплера. Теперь же изменение частоты приходящего сигнала в совокупности с неизменностью разности фаз между точками наблюдения в интерферометре должно однозначно свидетельствовать об эффекте Доплера, а в совокупности с изменением разности фаз между этими точками – об изменении частоты неподвижного генератора.
Экспериментальные результаты, полученные в работе, стали возможны благодаря изобретению интерферометра с механическим делением луча лазера. Благодаря этому изобретению удалось впервые за всю историю СТО доказать несостоятельность преобразований Лоренца и опровергнуть постулат об инвариантности скорости света.
Авторы не нашли в известной им литературе аналогов рассмотренного интерферометра, поэтому ему и присвоено наименование представленное в названии статьи.
Благодарности
Авторы выражают большую благодарность Валерию Александровичу Невольниченко за помощь в изготовлении интерферометра.
Литература
1. Albert A. Michelson, Edward W. Morley. On the Relative Motion of the Earth and the Luminiferous Ether. The American Journal of Science. III series. Vol. XXII, No. 128, p.120 – 129.
2. Лансберг Г. С. Оптика. Учеб. Пособие. Для вузов. – 6-е изд. Стериотип. – М,: ФИЗМАТЛИТ, 2003, – 848 с.
3. Petr Beckmann, Peter Mendics. Test of the Constancy of the Velocity of Electromagnetic Radiation in Rig h Vacuum. RADIO SCIENCE Journal of Research NBS/USNC-URSI Vo!’ 69D, No.4, April 1965.
4. De-Sitter W. Ein astronomischer Beweis fur die Konstanz der Lichtgeschwindigkeit // Physikalisch Zeitschrift.-1913. B.14. S.429; S. 1267-1268.
5. Majorana Q. Experimental demonstration of the constancy of velocity of light emitted by a moving source // Lincei Rendues. 1918, v.27, pp. 402 – 406; Physical Review. 1918. v. 11, pp. 411 – 420; Philosophical Magazine. 1919, v. 37, pp. 145 – 150.
6. Wallace Kantor . Direct First-Order Experiment on the Propagation of Light from a Moving Source . Journal of the Optical Society of America, 1962, v.52, Issue 9, pp. 978-984.
7. Ray O. Waddoups, W. Farrell Edwards, and John J. Merrill. Experimental Investigation of the Second Postulate of Special Relativity. Journal of the Optical Society of America, 1965, v.55, Issue 2, pp. 142-143.
8. Farley F., Kjellman J., Wallin J. Test of the second postulate relativity in the GeV region, Physical Letters, 1964, v. 12, No. 3, pp. 260 -262.
9. Fillipas T. A., Fox J. G. Velocity of gamma rays from a moving source, Physical Review. 1964, v. 135, pp. 1071 – 1075.
10. Babcock G. C., Bergman T. G. Determination of the constancy of the speed of light // Journal of Optical Society of America. – 1964. – v. 54. No. 2. – p. 147 – 151.
11. Fox J. G. Experimental Evidence for the Second Postulate of Special Relativity. American Journal of Physics, 1962 v. 30, pp. 297.
12. Экспериментальные основания теории относительности. С. И. Вавилов. Собрание сочинений. Т. 4. — М.: Изд-во АН СССР, 1956.
13. Гинзбург В. Л. Как и кто создал теорию относительности? в Эйнштейновский сборник, 1966. – М.: Наука, 1966. – c. 366-378. – 375 с.
14. Менде Ф. Ф. Дубровин А. С. Альтернативная идеология электродинамики. Монография. М.: Перо, 2016. – 198 с.
Ф. Ф. Менде
Украина, Харьков
E-mail: fedormende@gmail.com
