
«Пока законы математики остаются определёнными, они не имеют ничего общего с реальностью; как только у них появляется нечто общее с реальностью, они перестают быть определёнными» (Альберт Эйнштейн)
«Чистая математика — это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, что мы говорим» (Бертран Рассел)
«Никоим образом не может быть, чтобы аксиомы, установленные рассуждением, имели силу для открытия новых дел, ибо тонкость природы во много раз превосходит тонкость рассуждений» (Фрэнсис Бэкон)
Многие интеллектуалы склонны называть математику «царицей наук» и преподносить её теоремы как абсолютную истину, полученную чисто логическим дедуктивным выводом безотносительно физической реальности, не опираясь на эмпирические данные. Якобы математические объекты существуют вне пространства-времени, в разуме Бога или в платоновском мире идей, а мы лишь открываем вечные истины. Говорят, наше сознание имеет прямой доступ к этому миру математических абстракций посредством интуиции – не иначе, как божественного откровения или снисхождения самой истины, открывающейся только тем, кто её достоин.

Объективный идеализм Платона
Все философские учения, постулирующие существование независимой от воли и разума субъекта нематериальной реальности, объединяют под общим названием «объективный идеализм», его основа – платонизм.
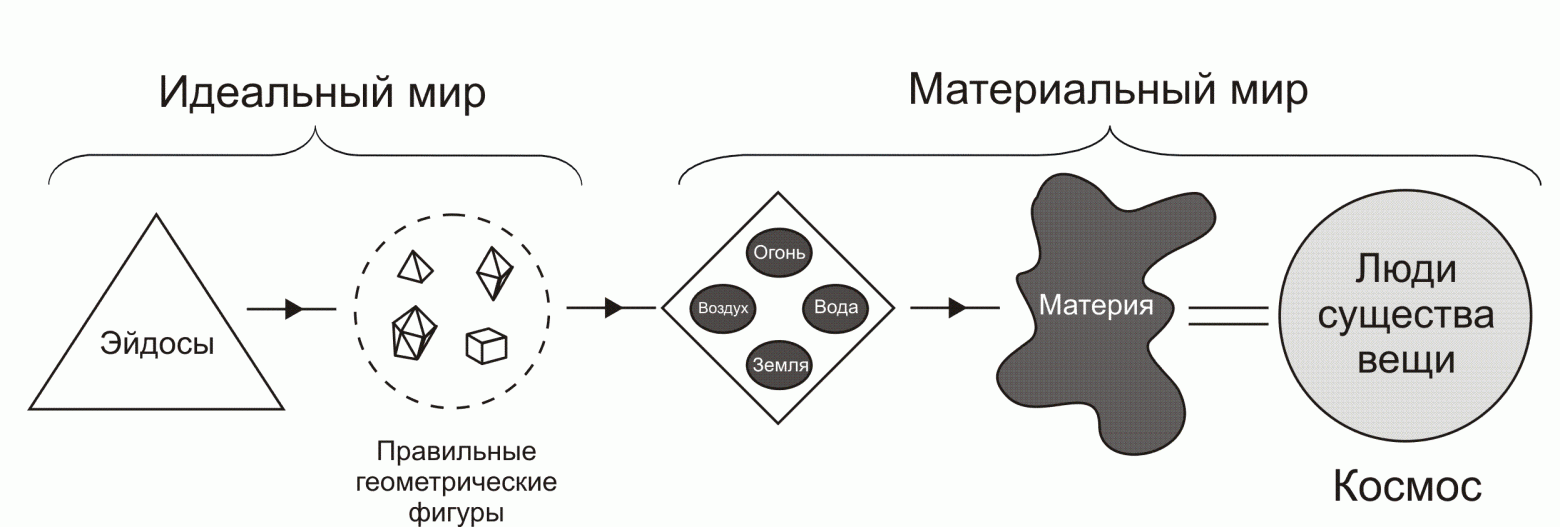
Под влиянием платонизма находились как средневековая христианская схоластика, так и вся европейская идеалистическая философия нового времени, и наука XX века.
Платоновский идеализм всё ещё имеет много сторонников, особенно в религиозных и эзотерических кругах. Так, по результатам опроса 2020 г., проведенного журналом PhilPapers, 38% философов проголосовали за платонизм, 42% – за номинализм (остальные выбрали «другое»), но среди философов математики это соотношение составило 53% против 25%. Даже среди учёных, строго следующих научному методу, до сих пор распространено убеждение, что математическое знание происходит из особого источника, называемого математической интуицией, и обладает абсолютной определённостью.
В представлении обычного человека математика – это наука о числах и геометрических фигурах. Но в большинстве работ по математике вы не найдёте ни того, ни другого – сплошные буквы и непонятные знаки математической логики. Теоремы высшей математики настолько абстрактны, что невозможно объяснить о чём они.
Эрнест Нагель и Джеймс Ньюман в книге “Теорема Гёделя” пишут следующее:
«…математика есть попросту наука, изучающая получение логических следствий из некоторых заданных аксиом, или постулатов. Фактически стало общепризнанным то обстоятельство, что математические выводы и заключения не имеют никакого другого смысла, помимо того в некотором роде специального смысла, который связан с терминами или выражениями, входящими в постулаты. Таким образом, математика оказалась даже еще значительно более абстрактной и формальной наукой, чем это было принято считать: более абстрактной — поскольку математические предложения в принципе могут быть истолкованы скорее как утверждения о чем угодно, а не как утверждения, относящиеся к некоторым фиксированным множествам предметов и неотъемлемым свойствам этих предметов; более формальной — поскольку правильность математических доказательств гарантируется чисто формальной структурой некоторых предложений, а отнюдь не содержанием этих предложений»
Общепринятый аксиоматический метод состоит в том, что за основу берётся несколько самоочевидных аксиом (постулатов), которые принимаются без доказательств, и из них при помощи силлогизмов выводятся теоремы. Математическое утверждение считается истинным, если оно чётко сформулировано в виде теоремы и доказано с помощью последовательности силлогизмов (правил вывода), посылками которых являются аксиомы или уже доказанные теоремы. Вся эта формальная система из аксиом, теорем, доказательств и алгоритмов должна быть однозначной и непротиворечивой. Проблема в том, что мы не можем на собственном опыте убедиться в существовании математических объектов (чисел, фигур, множеств, функций). Ничто вне или внутри математики не доказывает и не объясняет необходимости её выводов. Почему же мы безоговорочно принимаем математические теоремы и считаем их необходимо истинными?
С античности и до начала научной революции XVII века первоисточниками математики считались «Органон» Аристотеля и «Начала» Евклида. Аристотель заложил основы формальной логики и теории доказательств, утверждая, что все обоснованные доказательства можно выразить в виде силлогизмов. У Евклида геометрия и теория чисел были сформулированы как единая аксиоматическая система, в которой из исходных предположений (постулатов или аксиом) с помощью выделенного набора логических средств выводились следствия о свойствах первичных понятий (точка, прямая, число и т. д.) и конструируемых из них объектов (геометрические фигуры). Но в евклидовой геометрии оставалась спорной пятая аксиома (через точку вне прямой можно провести только одну прямую, параллельную первой). Но в XIX веке Гаусс и Лобачевский пятый постулат замении на противоположный, и получили неевклидову геометрию, никак не связанную с реальностью.
Изобретение в конце XVII века Ньютоном и Лейбницем интегрального и дифференциального исчисления с бесконечно большими и бесконечно малыми величинами заложило основу математического анализа, основным инструментом которого стали функции – отношения зависимости одной переменной величины от другой. В 1806 г. Андре-Мари Ампер предположил, что любая непрерывная функция должна быть дифференцируемой (регулярной и монотонной) всюду, за исключением некоторых отдельных значений аргумента, поскольку у любой непрерывной кривой можно найти градиент для любого конечного числа точек. Однако в 1872 г. была открыта функция Вейерштрасса, которая непрерывна, но нигде не дифференцируема. Она поставила под сомнение всё, что математики думали о математическом анализе прежде: Анри Пуанкаре назвал её «оскорблением здравого смысла», Шарль Эрмит – «безобразным злом», а Эмиль Пикар сказал, что если бы Ньютон знал о таких функциях, то не создал бы математический анализ.
Это натолкнуло математиков искать “мысли мирового разума” не в числах и геометрических фигурах, а в абстрактных объектах. Такими элементарными идеализированными объектами, из которых можно построить все остальные объекты, стали множества.
В конце XIX века Георг Кантор разработал теорию множеств – новый язык математики, своего рода математическую «теорию всего». Само множество в этой теории является базовым неопределимым понятием, но неформально так называют любую совокупность объектов, обладающих каким-то общим свойством – элементов множества. Количество элементов обобщается понятием мощности множества и может быть нулевым (пустое множество), конечным или бесконечным. Множества считаются равномощными, если между их элементами можно установить взаимно-однозначное соответствие (биекцию). Теория множеств позволяла вывести всю формальную арифметику, вещественные числа, анализ и геометрию из одного понятия пустого множества и свойства отношения (принадлежности). Например, все натуральные и вещественные числа можно получить вложением друг в друга фигурных скобок, обозначающих пустое множество: {} – это 0, {{}} – это 1, {{{}}} – это 2 и т.д. Из операций пересечения, объединения и разности множеств можно вывести операции «и», «или» и «не» в алгебре логики. Но самые интересные следствия постулатов Кантора относились к бесконечным множествам, которые равномощны каждому из своих подмножеств.
До Кантора была известна только одна бесконечность – потенциальная бесконечность натурального ряда, которой интересовались скорее философы и теологи, чем математики, поскольку она считалась недоступной человеческому разуму: как говорил Декарт, «бесконечность распознаваема, но не познаваема». Однако в 1874 г. Кантор доказал, что множество вещественных чисел «бесконечнее» множества натуральных чисел, то есть между элементами этих множеств невозможно установить взаимно-однозначное соответствие. Если множество натуральных чисел является счётным, то множество действительных (континуум) несчётно бесконечно – не существует способа пересчитать его элементы или найти среди них наименьшее число. Более того, Кантор показал, что множество всех подмножеств (булеан) любого бесконечного множества всегда бесконечнее этого множества (теорема Кантора), следовательно, существует бесконечное множество уровней бесконечности. Для обозначения этих уровней или мощности бесконечных множеств он ввёл кардинальные числа: ℵ₀ (алеф-нуль) для счётной бесконечности, ℵ₁ (алеф-один) для континуума, и т.д. Они обозначают только количество элементов множества, а для указания порядка элемента, чтобы можно было продолжить счёт после достижения бесконечности, Кантор придумал ординальные числа, обозначаемые буквой ω.
Конечно выяснилось, что теория множеств противоречива и содержит всевозможные парадоксы. Первый парадокс обнаружил сам Кантор в 1895 г., когда решил рассмотреть множество всех множеств. Если оно содержит абсолютно все множества, то среди них будет и множество всех его подмножеств, которое по теореме Кантора должно быть больше самого множества всех множеств. Затем в 1901 г. Бертран Рассел рассмотрел множество всех множеств, которые не содержат сами себя, и задал вопрос: будет ли это множество содержать само себя? Как положительный, так и отрицательный ответ ведут к противоречию, которое назвали парадоксом Рассела. Кантор предложил разделить все множества на противоречивые и непротиворечивые, исключив первые из теории. Рассел предложил называть кардинальные и ординальные числа не множествами, а собственными классами, и в 1908 г. ранжировал все множества в своей теории типов. Другие математики стали вводить дополнительные аксиомы, запрещающие построение противоречивых множеств. Так на смену «наивной» теории множеств Кантора пришла усовершенствованная теория множеств Цермело-Френкеля (ZF), которая используется с дополнением в виде аксиомы выбора (ZFC).
Аксиома выбора утверждает: для любого семейства непустых множеств существует множество, которое содержит по одному элементу из каждого множества семейства. Для конечного семейства конечных множеств эта аксиома не требуется, но в случае с бесконечным несчётным множеством не существует способа выбрать определённый его элемент. То есть аксиома не предъявляет конкретной функции выбора, а лишь утверждает её существование – любое бесконечное множество можно вполне упорядочить и перебрать элемент за элементом. Кроме того, как иногда шутят, аксиома выбора говорит, что у вас есть выбор, принимать аксиому выбора или нет. Как заметил Бертран Рассел, «Сначала она кажется очевидной; но чем больше вдумываешься, тем более странными кажутся выводы из этой аксиомы; под конец же вообще перестаешь понимать, что же она означает». Например, из аксиомы выбора следует парадокс Банаха-Тарского: можно разрезать шар на конечное число кусков и собрать из этих кусков два точно таких же шара. Причём для разбиения шара аксиома выбора используется континуум раз.
Ещё одной неразрешимой проблемой была гипотеза континуума, стоявшая под номером 1 в списке из 23-х якобы важнейших задач столетия, представленном в 1900 году Давидом Гильбертом на Всемирной конференции математиков в Париже. Континуум-гипотеза, выдвинутая в 1877 году Георгом Кантором, предполагала, что любое бесконечное подмножество континуума является либо счётным, либо континуальным. Иначе говоря, между счётным множеством и континуумом нет других множеств промежуточной мощности. Оказалось, что эта гипотеза независима от системы Цермело-Френкеля. В 1940 году Курт Гёдель доказал, что она не может быть опровергнута, а в 1963 году Пол Коэн доказал, что она не может быть доказана. То есть существуют разные математики: в одной континуум-гипотеза верна, а в других между счётной бесконечностью и континуумом можно поместить любое конечное число бесконечных множеств промежуточной мощности.
Обнаруженные к началу XX века противоречия в теории Кантора спровоцировали очередной кризис оснований математики, усугублённый тем, что большинство полученных к тому времени математических доказательств не соответствовали стандартам определённости и строгости и не могли быть выражены в виде чистой последовательности силлогизмов. В попытках разрешения этого кризиса возникли три направления в философии математики: интуиционизм, логицизм и формализм. Все три школы пытались свести математику к теоремам о свойствах натуральных чисел и обосновать непротиворечивость арифметики Пеано. Впоследствии возникли и другие направления философии математики, включая психологизм, фикционализм, артистизм и социальный конструктивизм, которые мы не будем рассматривать из-за их очевидного антиреализма: это ещё раз показало, что математика является чистой выдумкой, фикцией, всеобщей договорённостью, формой искусства или развлечением.
Как говорил основатель школы интуиционистов, голландский математик Лейтзен Эгберт Ян Брауэр, «Математика – свободное творчество, независимое от опыта; она создаётся из единственной априорной интуиции, которую можно назвать «постоянством в изменении», или «единством в множественности»». Его ученик Аренд Гейтинг разработал особую интуиционистскую логику, отрицающую закон исключённого третьего и доказательства от противного для бесконечных множеств. Ведь по мнению интуиционистов, логика – часть математики, и её правила можно ограничивать. Дальнейшим развитием данного подхода стала конструктивная математика.
Конструктивисты считают реальными лишь те математические сущности, которые могут быть сконструированы явно – например, вычислены на бумаге или на компьютере. Только вопросы, касающиеся поведения конечных алгоритмов, имеют смысл и должны исследоваться в математике. Крайней формой конструктивизма является финитизм, отрицающий существование математических объектов, которые нельзя построить из натуральных чисел за конечное число шагов. Например, все натуральные числа принимаются как существующие, а множество всех натуральных чисел не считается существующим как математический объект – бесконечности нет места ни во Вселенной, ни в человеческом мышлении. А крайней формой финитизма является ультрафинитизм, отрицающий даже конечные величины, которые невозможно построить с помощью имеющихся физических ресурсов.
В середине XIX века были сформулированы законы де Моргана и алгебра логики Джорджа Буля, позволявшая выразить логику Аристотеля в виде формул и алгебраических операций, а в 1870-х гг. Чарльз Сандерс Пирс и Готтлоб Фреге расширили исчисление высказываний, введя квантификаторы для построения логики предикатов. Возникла идея, что вся математика сводится к логике и является её частью, а значит, все математические утверждения являются необходимыми логическими истинами. Как говорил Готлоб Фреге, «арифметика есть лишь дальнейшее развитие логики, а каждое арифметическое предложение есть логический закон, хотя и производный». Теоремы математики могут быть выведены из логических аксиом посредством чисто логической дедукции, а концепции математики могут быть выведены из логических концепций посредством явных определений. Натуральные числа – логические абстракции, а не физические объекты или их свойства.
Фреге указал на три желаемых свойства логической теории: непротиворечивость (невозможность доказательства противоречивых утверждений), полнота (любое утверждение либо доказуемо, либо опровержимо; то есть его отрицание доказуемо) и разрешимость (существует процедура принятия решения для проверки каждого утверждения). Отсюда возникла идея вывести всю математику из формальной логики, приняв за основу минимальное количество аксиом. Естественно, такая система должна была быть непротиворечивой, полной и не содержать парадоксов. Результатом программы Фреге стал монументальный трёхтомный труд Бертрана Рассела и Альфреда Уайтхеда Principia Mathematica (1910-1913). Его авторам удалось избежать импредикативных определений и парадокса Рассела с помощью теории типов, в которой невозможно было сформулировать понятие множества всех множеств. Однако построенная ими формальная система оказалась слишком громоздкой (доказательство того, что 1+1=2, заняло 379 страниц) и включала дополнительные постулаты, невыводимые из логики: аксиому бесконечности (существует бесконечное число объектов) и аксиому сводимости (для каждого множества существует равнообъёмное ему множество первого порядка).
Дальше всех в деле аксиоматизации математики зашёл Давид Гильберт, который пытался доказать полноту и непротиворечивость финитной арифметики средствами самой арифметики, «исключив при этом из неё всю метафизику». «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу». «Все высказывания, которые составляют вместе математику, превращаются в формулы, так что сама математика превращается в совокупность формул». В такой формальной системе, состоящей из множества аксиом, правил вывода и алфавита формального языка для их записи, любое утверждение либо истинно, либо ложно, и третьего не дано. Теорема истинна, если её можно вывести из аксиом, применяя правила вывода (формальное доказательство). Математические утверждения – это утверждения не о числах, множествах, фигурах и т.п., а о последствиях определённых правил манипуляции строками. То есть по сути математика – это просто механическая игра символами, не имеющими смысла. Гильберт считал, что любая теорема о конечных математических объектах, которая может быть получена с использованием идеальных бесконечных объектов, может быть получена и без них конечным числом операций, поэтому допущение бесконечных математических объектов не вызовет проблем относительно конечных объектов.
В списке проблем Гильберта, которые, как он надеялся, математики смогут решить в XX веке, под номером 2 стояла задача «раз и навсегда установить определённость математических методов», найдя набор правил вывода, достаточный для всех обоснованных доказательств, и затем доказать состоятельность этих правил в соответствии с их собственными нормами. Гильберт хотел сформулировать строгую теорию доказательства, при условии, что доказательства в этой теории должны быть конечными, т.е. в них должен использоваться фиксированный и конечный набор правил вывода, они должны начинаться с конечного числа конечно выраженных аксиом и содержать лишь конечное число конечных элементарных шагов. Теоретически эти правила делали бы доказуемым любое истинное математическое утверждение и недоказуемым любое ложное утверждение. В таком случае машина, способная выучить правила вывода, смогла бы оценивать математические высказывания лучше, чем самый одарённый математик, и делать математические открытия, даже не понимая значения символов и того, что она доказывает – просто проверяя все возможные строки букв, чисел и математических символов, пока одна из них не пройдёт проверку на то, является ли она доказательством какой-нибудь недоказанной гипотезы. Это была бы плохая новость не только для математиков, но и для учёных вообще, поскольку она бы устранила необходимость понимания математических идей и сделала бы возможным существование абсолютных истин, защищённых от критики.
Гильберт был неправ. В 1931 году 25-летний австрийский математик Курт Гёдель в статье «О формально неразрешимых предложениях Principia Mathematica и связанных с ней системах I» доказал, что 2-я задача Гильберта не имеет решения – невозможно доказать все теоремы формальной системы арифметики с помощью синтаксических правил вывода, применённых к аксиомам.
Тем самым Курт Гёдель нанёс сокрушительный удар не только по Principia Mathematica и программе Гильберта, но и по любой другой аксиоматической системе подобного рода: он показал, что никакая формализованная система логики не может быть адекватной базой математики.
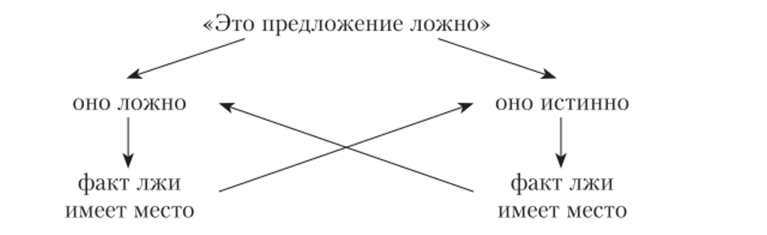
Гёдель сформулировал две теоремы о неполноте: «слабую» и «сильную». Обе касаются пределов доказуемости в формальных аксиоматических теориях математической логики. Речь идёт о теориях, «достаточно мощных», чтобы содержать как подсистему элементарную арифметику, которая сама по себе достаточно богата, чтобы выразить универсальность, отрицание и самоотнесение.
Первая теорема Гёделя о неполноте: «любая достаточно мощная непротиворечивая формальная система аксиом, теоремы которой могут быть перечислены эффективной процедурой (алгоритмом), содержит утверждения, которые истинны, но недоказуемы внутри системы». Любая формальная система, содержащая элементарную арифметику, фундаментально неполна, т.е. в ней нельзя доказать все истинные утверждения. Если формальная арифметика непротиворечива, то в ней существует невыводимая и неопровержимая формула, на которой арифметика и построена.
Вторая теорема Гёделя о неполноте: «любая достаточно мощная непротиворечивая система аксиом не может доказать свою собственную непротиворечивость». Логическая полнота или неполнота системы тоже не может быть доказана в рамках этой системы – для её доказательства или опровержения требуется усилить систему дополнительными аксиомами. Чтобы доказать, что аксиоматическая система математики непротиворечива, нужно предположить непротиворечивость системы, которая сильнее, чем система, непротиворечивость которой доказывается. Любая система, достаточно мощная, чтобы доказать непротиворечивость арифметики, по крайней мере так же мощна, как сама арифметика.
С помощью диагонального метода Кантора Гёдель показал, что практически все математические истины не имеют доказательства – они недоказуемы. Из этого следовало, что практически все математические высказывания неразрешимы: ни для их истинности, ни для их ложности доказательства нет. Каждое из них либо верно, либо ложно, но с помощью физических объектов, таких как мозг или компьютер, это никак невозможно выяснить. Показательно, что все неразрешимые высказывания прямо или косвенно относятся к бесконечным множествам. Но лишь об очень немногих вопросах известно, что они неразрешимы, хотя на самом деле таковыми является большинство. Существует много недоказанных математических предположений, и некоторые из них вполне могут оказаться неразрешимыми. Но есть ещё одно определение неразрешимости, принятое в теории вычислений. Оно относится к проблемам принятия решений, которые представляют собой счётные бесконечные списки вопросов, каждый из которых требует ответа «да» или «нет». Такая проблема называется неразрешимой, если не существует вычислимой функции, которая правильно отвечает на каждый вопрос в списке.
Проблема алгоритмической разрешимости и задача остановки
В 1928 гоу Давид Гильберт поставил перед математиками ещё одну задачу, известную как проблема разрешимости (нем. Entscheidungsproblem): найти алгоритм, который принимал бы в качестве входных данных описание формального языка и математического утверждения, и, после конечного числа шагов, останавливался бы и выдавал один из двух ответов: «истина» или «ложь», в зависимости от того, истинно утверждение или ложно. То есть алгоритм давал бы однозначный ответ да/нет на любой заданный вопрос, отделяя истинные математические утверждения от ложных. Для решения задачи разрешимости требовалось формализовать понятия алгоритма и эффективно вычислимой функции. В середине 1930-х гг. было предложено сразу несколько вычислительных моделей: лямбда-исчисление Алонзо Чёрча, машина Тьюринга, машина Поста и общие рекурсивные функции Стивена Клини. Впоследствии оказалось, что все они эквивалентны по своим возможностям, т.е. имеют одинаковый репертуар вычислимых функций – являются тьюринг-полными. Так появилась теория алгоритмов, которая послужила механизмом и основой для любой математики и для любых вычислений возможных в принципе.
В 1936 г. 23-летний аспирант Чёрча в Принстоне Алан Тьюринг опубликовал статью «О вычислимых числах в приложении к проблеме разрешимости», в которой ввёл понятие абстрактной вычислительной машины (той самой машины Тьюринга) и доказал теорему о неразрешимости задачи остановки, заложив теоретическую основу компьютерных наук. Тьюринг первым предложил модель машины, способной выполнить любую конечную, эффективную процедуру (алгоритм). На тот момент была известна только одна подобная машина – компьютер, или «человек, снабжённый бумагой, карандашом и ластиком и подчинённый строгой дисциплине». Ключевая идея Тьюринга заключалась в том, что результат вычисления не зависит от конкретной физической реализации компьютера, поэтому вся работа человеческого компьютера может быть имитирована логической машиной, каждая операция которой представляет собой «некоторое изменение физической системы, состоящей из компьютера и его ленты».
Машина Тьюринга — абстрактный исполнитель, состоящий из бесконечной разделённой на ячейки бумажной ленты и головки записи-чтения, которая двигается вдоль ленты, считывая и перезаписывая символ в текущей клетке в соответствии с таблицей правил. Для каждого текущего символа и каждого состояния головки у неё есть инструкция, какой символ записать и в какую сторону сдвинуться. Такая таблица правил является примитивным языком программирования. Машина может перейти в конечное состояние остановки, в котором она принимает или отклоняет ввод, или попасть в бесконечный цикл и продолжать читать ленту вечно. Алгоритм – это последовательность однозначных инструкций (программа) на каком-либо языке программирования, которая за конечное число шагов переводит входные данные в результат (да/нет) и завершает свою работу. Если на каких-то начальных данных программа зацикливается, то алгоритма она не описывает. Тьюринг показал, что функция вычислима, если для неё существует алгоритм, который может быть определён машиной Тьюринга. Каждое корректное доказательство можно преобразовать в вычисление, которое получает вывод, начиная с исходных допущений, а каждое правильно выполненное вычисление доказывает, что выходные данные – это результат выполнения заданных операций над входными данными.

Проблема разрешимости Гильберта сводилась к вопросу о том, разрешима ли логика первого порядка – существует ли алгоритм, который определяет, является ли любая заданная логическая формула первого порядка теоремой. Чёрч и Тьюринг доказали, что такого алгоритма не существует – нет и не может быть вычислительной машины, получающей на входе любую формулу функционального исчисления, выполняющей конечное число шагов и выдающей правильный ответ, доказуема эта формула в функциональном исчислении или нет. На языке теории вычислений проблема применимости алгоритма называется задачей остановки – требуется найти общий метод, который позволял бы для произвольной машины Тьюринга и произвольного начального состояния её ленты определить, остановится машина или нет. Вам даётся описание программы и её начальные входные данные. Нужно выяснить, завершится ли когда-либо выполнение программы с этими данными, или программа будет работать вечно без остановки. Тьюринг доказал, что ни одна машина не может решить эту задачу, если сама не выполнит данную программу. Согласно теореме Тьюринга, не существует машины Тьюринга, которая предсказывала бы для любой другой машины Тьюринга, остановится она на определённом входе или нет. Иначе говоря, для машины Тьюринга набор входов, на которых она останавливается за конечное время, невычислим. На практике это означает, что компьютеру всегда можно поставить задачу, которую он не сможет решить, не уходя в бесконечный перебор, поскольку не сможет ни подтвердить, ни опровергнуть данное утверждение. Не получится запрограммировать компьютер так, чтобы он мог доказать все гипотезы арифметики.
Алан Тьюринг доказал свою теорему всё тем же диагональным методом, который Курт Гёдель применял в доказательстве теорем о неполноте, а Георг Кантор – в доказательстве того, что существуют бесконечно большие множества, превышающие бесконечность натуральных чисел. Анализируя список всех возможных машин, работающих на основе описаний всех возможных машин, Тьюринг пришёл к выводу, что практически все математические функции, которые логически могут существовать, нельзя вычислить никакой программой. Они невычислимы, потому что множество всех функций – несчётно бесконечно, а множество программ – лишь счётно бесконечно. Поскольку алгоритм вычисления должен состоять из конечного числа шагов, т.е. из конечной последовательности символов какого-либо алфавита, множество таких последовательностей можно посчитать, и оно бесконечно меньше множества всех логически возможных математических структур. Невычислимых функций несоизмеримо больше, чем вычислимых.
Доказательство существования невычислимых функций в классе машин Тьюринга было аналогично результату Гёделя о неполноте элементарной арифметики, поскольку машина Тьюринга формализует понятие вычисления и, следовательно, содержит элементарную арифметику. Класс машин Тьюринга достаточно богат, чтобы выразить универсальность, отрицание и самореференцию – функции, ссылающиеся сами на себя. Рекурсивные функции – это элементарные арифметические функции, работающие с натуральными числами: сложение, вычитание, умножение и деление, а также все другие функции, которые могут быть определены через них. Любая достаточно мощная формальная система содержит арифметику в качестве подсистемы и может быть представлена в виде элементарных арифметических функций. Такая система способна рассуждать о своих собственных функциях и доказательствах, но поскольку она непротиворечива, она по необходимости является неполной. Впоследствии Стивен Клини показал, что существование полной и непротиворечивой эффективной системы арифметики означало бы разрешимость проблемы остановки, т.е. существование алгоритма, который всегда мог бы проверить истинность или ложность арифметического высказывания.
***
«Непостижимая эффективность математики в описании реальности» – мантра бесконечно повторяемая математиками. В реальности обычно математические формулы не совмещаются с наблюдениями без перенормировки, то есть подгонки под ответ… Математика это язык символов, аналогичных иероглифам, и написать этими символами можно любую мысль, как истинную, так и ложную.
